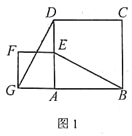
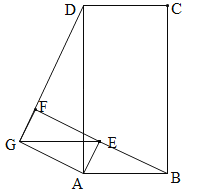
【题目】如图1,正方形ABCD和正方形AEFG,连接DG,BE。
(1)发现
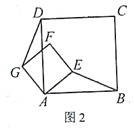
当正方形AEFG绕点A旋转,如图2,①线段DG与BE之间的数量关系是____________。②直线DG与直线BE之间的位置关系是____________。
(2)探究
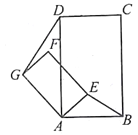
如图3,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE,证明:直线DG⊥BE
(3)应用
在(2)情况下,连结GE(点E在AB上方),若GE∥AB,且AB=![]() ,AE=1,则线段DG是多少?(直接写出结论)
,AE=1,则线段DG是多少?(直接写出结论)
参考答案:
【答案】 DG=BE DG⊥BE
【解析】试题分析:(1)证明△EAB≌△GAD,可得到BE=DG,∠ABE=∠ADG,再由三角形内角和为180°,即可得到结论;
(2)证明△ABE∽△ADG,再由三角形内角和为180°,即可得到结论;
(3)当GE∥AB时,B、E、F三点在一条直线上,且F刚好在DG上.先求出AD,AG的长,再由勾股定理即可得到结论.
试题解析:解:(1)①DG=BE;②DG⊥BE.理由如下:
延长BE交AD,DG分别为P,H.∵四边形ABCD和四边形AEFG都是正方形,∴AB=AD,∠BAD=90°,AE=AG,∠EAG=90°,∴∠EAB=∠GAD.在△EAB和△GAD中,∵AB=AD,∠EAB=∠GAD,AE=AG,∴△EAB≌△GAD,∴BE=DG,∠ABE=∠ADG.∵∠APB=∠HPD(对顶角相等),∴∠BAP=∠DHP=90°,∴BG⊥DG.
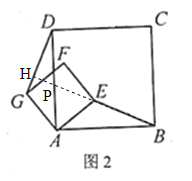
(2)延长BE交AD,DG分别为P,H.
∵∠BAE+∠DAE=∠DAG+∠DAE=90°,∴∠BAE=∠DAG.
∵AD=2AB,AG=2AE,∴![]() ,∴△ABE∽△ADG,∴∠ABP=∠HDP.
,∴△ABE∽△ADG,∴∠ABP=∠HDP.
∵∠APB=∠HPD,∴∠BAD=∠DHP=90°,∴ DG⊥BE.
(3) 当GE∥AB时,B、E、F三点在一条直线上,且F刚好在DG上,∴∠AEB=90°.∵∠AGD=∠AEB,∴∠AGD=90°.∵AB=![]() ,AE=1,∴AG=2AE=2,AD=2AB=
,AE=1,∴AG=2AE=2,AD=2AB=![]() ,∴DG=
,∴DG=![]() =
=![]() =4.
=4.
-
科目: 来源: 题型:
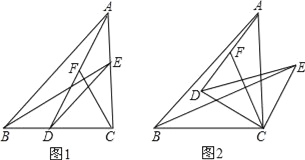
查看答案和解析>>【题目】已知△ABC和△DEC都是等腰直角三角形,C为它们的公共直角顶点,D、E分别在BC、AC边上.
(1)如图1,F是线段AD上的一点,连接CF,若AF=CF;
①求证:点F是AD的中点;
②判断BE与CF的数量关系和位置关系,并说明理由;
(2)如图2,把△DEC绕点C顺时针旋转α角(0<α<90°),点F是AD的中点,其他条件不变,判断BE与CF的关系是否不变?若不变,请说明理由;若要变,请求出相应的正确结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】周末,小明乘坐家门口的公交车到和平公园游玩,他先乘坐公交车
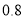 小时后达到书城,逗留一段时间后继续坐公交车到和平公园,小明出发一段时间后,小明的妈妈不放心,于是驾车沿相同的路线前往和平公园.如图是他们离家的路程
小时后达到书城,逗留一段时间后继续坐公交车到和平公园,小明出发一段时间后,小明的妈妈不放心,于是驾车沿相同的路线前往和平公园.如图是他们离家的路程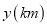 与离家时间
与离家时间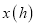 的关系图,请根据图回答下列问题:
的关系图,请根据图回答下列问题:
(1)小明家到和平公园的路程为
 ,他在书城逗留的时间为 _
,他在书城逗留的时间为 _ ;
;(2)图中
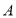 点表示的意义是 ;
点表示的意义是 ;(3)求小明从书城到和平公园的平均速度和小明的妈妈驾车的平均速度(平均速度
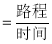 )
) -
科目: 来源: 题型:
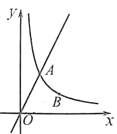
查看答案和解析>>【题目】如图,直线y=2x与反比例函数
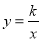 (k≠0,x>0)的图象交于点A(1,m),点B(n,t)是反比例函数图象上一点,且n=2t。
(k≠0,x>0)的图象交于点A(1,m),点B(n,t)是反比例函数图象上一点,且n=2t。(1)求k的值和点B坐标;
(2)若点P在x轴上,使得△PAB的面积为2,直接写出点P坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在矩形
 中,对角线
中,对角线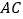 与
与 相交于点
相交于点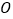 ,过点
,过点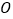 作直线
作直线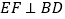 ,且交
,且交 于点
于点 ,交
,交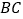 于点
于点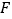 ,连接
,连接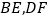 ,且
,且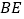 平分
平分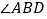 .
.①求证:四边形
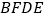 是菱形;
是菱形;②直接写出
 的度数;
的度数;
(2)把(1)中菱形
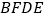 进行分离研究,如图2,
进行分离研究,如图2,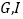 分别在
分别在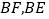 边上,且
边上,且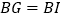 ,连接
,连接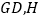 为
为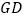 的中点,连接
的中点,连接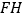 ,并延长
,并延长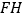 交
交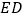 于点
于点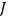 ,连接
,连接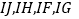 .试探究线段
.试探究线段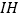 与
与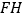 之间满足的关系,并说明理由;
之间满足的关系,并说明理由;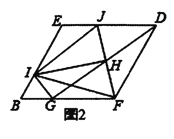
(3)把(1)中矩形
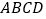 进行特殊化探究,如图3,矩形
进行特殊化探究,如图3,矩形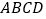 满足
满足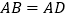 时,点
时,点 是对角线
是对角线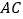 上一点,连接
上一点,连接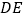 ,作
,作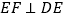 ,垂足为点
,垂足为点 ,交
,交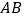 于点
于点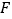 ,连接
,连接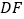 ,交
,交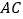 于点
于点 .请直接写出线段
.请直接写出线段 三者之间满足的数量关系.
三者之间满足的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx(a≠0)的图象过原点O和点A(1,
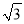 ),且与x轴交于点B,△AOB的面积为
),且与x轴交于点B,△AOB的面积为 。
。(1)求抛物线的解析式;
(2)若抛物线的对称轴上存在一点M,使△AOM的周长最小,求M点的坐标;
(3)点F是x轴上一动点,过F作x轴的垂线,交直线AB于点E,交抛物线于点P,且PE=
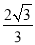 ,直接写出点E的坐标(写出符合条件的两个点即可)。
,直接写出点E的坐标(写出符合条件的两个点即可)。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知
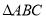 的三个顶点坐标分别是
的三个顶点坐标分别是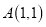 ,
,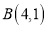 ,
,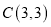 .
.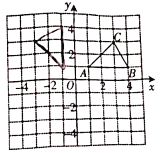
(1)将入
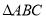 向下平移
向下平移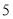 个单位后得到
个单位后得到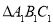 ,请画出
,请画出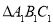 ;
;(2)将
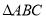 绕原点
绕原点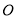 逆时针旋转
逆时针旋转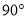 后得到
后得到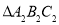 ,请画出
,请画出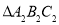 ;
;(3)判断以
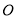 、
、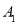 、
、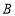 为顶点的三角形的形状.(无须说明理由)
为顶点的三角形的形状.(无须说明理由)
相关试题

