【题目】(1)如图1,在矩形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() ,过点
,过点![]() 作直线
作直线![]() ,且交
,且交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,且
,且![]() 平分
平分![]() .
.
①求证:四边形![]() 是菱形;
是菱形;
②直接写出![]() 的度数;
的度数;

(2)把(1)中菱形![]() 进行分离研究,如图2,
进行分离研究,如图2,![]() 分别在
分别在![]() 边上,且
边上,且![]() ,连接
,连接![]() 为
为![]() 的中点,连接
的中点,连接![]() ,并延长
,并延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .试探究线段
.试探究线段![]() 与
与![]() 之间满足的关系,并说明理由;
之间满足的关系,并说明理由;
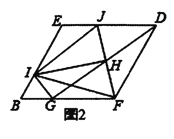
(3)把(1)中矩形![]() 进行特殊化探究,如图3,矩形
进行特殊化探究,如图3,矩形![]() 满足
满足![]() 时,点
时,点![]() 是对角线
是对角线![]() 上一点,连接
上一点,连接![]() ,作
,作![]() ,垂足为点
,垂足为点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() .请直接写出线段
.请直接写出线段![]() 三者之间满足的数量关系.
三者之间满足的数量关系.

参考答案:
【答案】(1)①见解析;②60°;(2)见解析;(3)见解析.
【解析】
(1)①由△DOE≌△BOF,推出EO=OF,由OB=OD,推出四边形EBFD是平行四边形,再证明EB=ED即可;②先证明∠ABD=2∠ADB,推出∠ADB=30°,即可解决问题;
(2)延长![]() 到
到![]() ,使得
,使得![]() ,连接
,连接![]() ,由菱形性质,
,由菱形性质,![]() ,得
,得![]() ,由此
,由此![]() ,由ASA可证得
,由ASA可证得![]() ,由此
,由此![]() ,故
,故
![]() ,由
,由![]() ,可证得
,可证得![]() 是等边三角形,可得
是等边三角形,可得![]() ,
,![]() ,由SAS可证
,由SAS可证![]() ,可得
,可得![]() ,即
,即![]() 是等边三角形,
是等边三角形,
在![]() 中,由
中,由![]() ,
,![]() ,可得
,可得![]() ,由此可得
,由此可得![]() ;
;
(3)结论:EG2=AG2+CE2.如图3中,将△ADG绕点D逆时针旋转90°得到△DCM,先证明△DEG≌△DEM,再证明△ECM是直角三角形即可解决问题.
(1)①证明:如图1中,
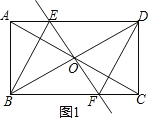
∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
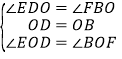 ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∵![]() ,
,
∴![]() ,
,
∴四边形![]() 是菱形.
是菱形.
②∵四边形![]() 是菱形,
是菱形,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() =
=![]() ,
,
∵四边形![]() 是矩形,
是矩形,
∴![]() A=
A=![]() ,
,
∴![]() +
+![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∴![]() ;
;
(2)结论:![]() .
.
理由:如图2中,延长![]() 到
到![]() ,使得
,使得![]() ,连接
,连接![]() .
.
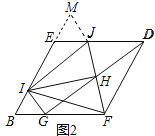
∵四边形![]() 是菱形,
是菱形,![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
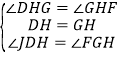 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,![]()
在![]() 和
和![]() 中,
中,
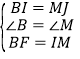 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
在![]() 中,∵
中,∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
(3)结论:![]() .
.
理由:如图3中,将△ADG绕点D逆时针旋转90°得到△DCM,
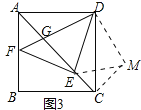
∵∠FAD+∠DEF=90°,
∴AFED四点共圆,
∴∠EDF=∠DAE=45°,∠ADC=90°,
∴∠ADF+∠EDC=45°,
∵∠ADF=∠CDM,
∴∠CDM+∠CDE=45°=∠EDG,
在△DEM和△DEG中,
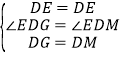 ,
,
∴△DEG≌△DEM,
∴GE=EM,
∵∠DCM=∠DAG=∠ACD=45°,AG=CM,
∴∠ECM=90°,
∴EC2+CM2=EM2,
∵EG=EM,AG=CM,
∴GE2=AG2+CE2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】周末,小明乘坐家门口的公交车到和平公园游玩,他先乘坐公交车
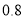 小时后达到书城,逗留一段时间后继续坐公交车到和平公园,小明出发一段时间后,小明的妈妈不放心,于是驾车沿相同的路线前往和平公园.如图是他们离家的路程
小时后达到书城,逗留一段时间后继续坐公交车到和平公园,小明出发一段时间后,小明的妈妈不放心,于是驾车沿相同的路线前往和平公园.如图是他们离家的路程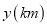 与离家时间
与离家时间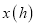 的关系图,请根据图回答下列问题:
的关系图,请根据图回答下列问题: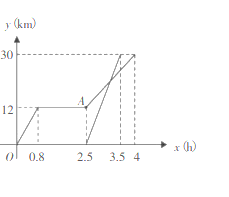
(1)小明家到和平公园的路程为
 ,他在书城逗留的时间为 _
,他在书城逗留的时间为 _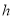 ;
;(2)图中
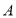 点表示的意义是 ;
点表示的意义是 ;(3)求小明从书城到和平公园的平均速度和小明的妈妈驾车的平均速度(平均速度
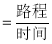 )
) -
科目: 来源: 题型:
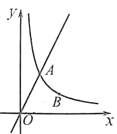
查看答案和解析>>【题目】如图,直线y=2x与反比例函数
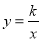 (k≠0,x>0)的图象交于点A(1,m),点B(n,t)是反比例函数图象上一点,且n=2t。
(k≠0,x>0)的图象交于点A(1,m),点B(n,t)是反比例函数图象上一点,且n=2t。(1)求k的值和点B坐标;
(2)若点P在x轴上,使得△PAB的面积为2,直接写出点P坐标。
-
科目: 来源: 题型:
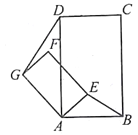
查看答案和解析>>【题目】如图1,正方形ABCD和正方形AEFG,连接DG,BE。
(1)发现
当正方形AEFG绕点A旋转,如图2,①线段DG与BE之间的数量关系是____________。②直线DG与直线BE之间的位置关系是____________。
(2)探究
如图3,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE,证明:直线DG⊥BE
(3)应用
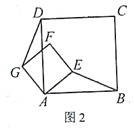
在(2)情况下,连结GE(点E在AB上方),若GE∥AB,且AB=
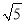 ,AE=1,则线段DG是多少?(直接写出结论)
,AE=1,则线段DG是多少?(直接写出结论)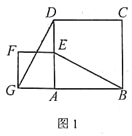
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx(a≠0)的图象过原点O和点A(1,
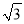 ),且与x轴交于点B,△AOB的面积为
),且与x轴交于点B,△AOB的面积为 。
。(1)求抛物线的解析式;
(2)若抛物线的对称轴上存在一点M,使△AOM的周长最小,求M点的坐标;
(3)点F是x轴上一动点,过F作x轴的垂线,交直线AB于点E,交抛物线于点P,且PE=
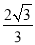 ,直接写出点E的坐标(写出符合条件的两个点即可)。
,直接写出点E的坐标(写出符合条件的两个点即可)。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知
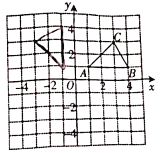
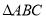 的三个顶点坐标分别是
的三个顶点坐标分别是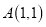 ,
,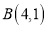 ,
,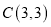 .
.
(1)将入
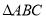 向下平移
向下平移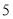 个单位后得到
个单位后得到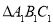 ,请画出
,请画出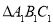 ;
;(2)将
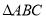 绕原点
绕原点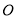 逆时针旋转
逆时针旋转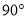 后得到
后得到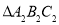 ,请画出
,请画出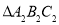 ;
;(3)判断以
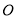 、
、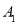 、
、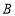 为顶点的三角形的形状.(无须说明理由)
为顶点的三角形的形状.(无须说明理由) -
科目: 来源: 题型:
查看答案和解析>>【题目】2017年12月8日,以“[数字工匠]玉汝于成,[数字工坊]溪达四海”为主题的2017一带一路数学科技文化节玉溪暨第10届全国三维数字化创新设计大赛(简称“全国3D大赛”)总决赛在玉溪圆满闭幕.某学校为了解学生对这次大赛的了解程度,在全校1300名学生中随机抽取部分学生进行了一次问卷调查,并根据收集到的信息进行了统计,绘制了下面两幅统计图.下列四个选项错误的是( )
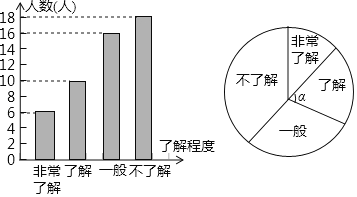
A. 抽取的学生人数为50人
B. “非常了解”的人数占抽取的学生人数的12%
C. a=72°
D. 全校“不了解”的人数估计有428人
相关试题

