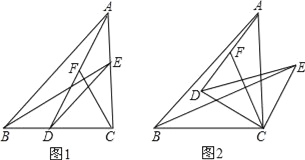
【题目】已知△ABC和△DEC都是等腰直角三角形,C为它们的公共直角顶点,D、E分别在BC、AC边上.
(1)如图1,F是线段AD上的一点,连接CF,若AF=CF;
①求证:点F是AD的中点;
②判断BE与CF的数量关系和位置关系,并说明理由;
(2)如图2,把△DEC绕点C顺时针旋转α角(0<α<90°),点F是AD的中点,其他条件不变,判断BE与CF的关系是否不变?若不变,请说明理由;若要变,请求出相应的正确结论.
参考答案:
【答案】(1)①证明见解析;②BE=2CF,BE⊥CF;(2)仍然有BE=2CF,BE⊥CF.
【解析】
(1)①如图1,由AF=CF得到∠1=∠2,则利用等角的余角相等可得∠3=∠ADC,然后根据等腰三角形的判定定理得FD=FC,易得AF=FD;
②先利用等腰直角三角形的性质得CA=CB,CD=CE,则可证明△ADC≌△BEC得到AD=BE,∠1=∠CBE,由于AD=2CF,∠1=∠2,则BE=2CF,再证明∠CBE+∠3=90°,于是可判断CF⊥BE;
(2)延长CF到G使FG=CF,连结AG、DG,如图2,易得四边形ACDG为平行四边形,则AG=CD,AG∥CD,于是根据平行线的性质得∠GAC=180°-∠ACD,所以CD=CE=AG,再根据旋转的性质得∠BCD=α,所以∠BCE=∠DCE+∠BCD=90°+α=90°+90°-∠ACD=180°-∠ACD,得到∠GAC=∠ECB,接着可证明△AGC≌△CEB,得到CG=BE,∠2=∠1,所以BE=2CF,和前面一样可证得CF⊥BE.
(1)①证明:如图1,
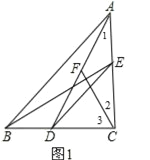
∵AF=CF,
∴∠1=∠2,
∵∠1+∠ADC=90°,∠2+∠3=90°,
∴∠3=∠ADC,
∴FD=FC,
∴AF=FD,
即点F是AD的中点;
②BE=2CF,BE⊥CF.理由如下:
∵△ABC和△DEC都是等腰直角三角形,
∴CA=CB,CD=CE,
在△ADC和△BEC中
 ,
,
∴△ADC≌△BEC,
∴AD=BE,∠1=∠CBE,
而AD=2CF,∠1=∠2,
∴BE=2CF,
而∠2+∠3=90°,
∴∠CBE+∠3=90°,
∴CF⊥BE;
(2)仍然有BE=2CF,BE⊥CF.理由如下:
延长CF到G使FG=CF,连结AG、DG,如图2,

∵AF=DF,FG=FC,
∴四边形ACDG为平行四边形,
∴AG=CD,AG∥CD,
∴∠GAC+∠ACD=180°,即∠GAC=180°﹣∠ACD,
∴CD=CE=AG,
∵△DEC绕点C顺时针旋转α角(0<α<90°),
∴∠BCD=α,
∴∠BCE=∠DCE+∠BCD=90°+α=90°+90°﹣∠ACD=180°﹣∠ACD,
∴∠GAC=∠ECB,
在△AGC和△CEB中
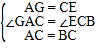 ,
,
∴△AGC≌△CEB,
∴CG=BE,∠2=∠1,
∴BE=2CF,
而∠2+∠BCF=90°,
∴∠BCF+∠1=90°,
∴CF⊥BE.
故答案为:(1)①证明见解析;②BE=2CF,BE⊥CF;(2)仍然有BE=2CF,BE⊥CF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平高集团有限公司准备生产甲、乙两种开关,共8万件,销往东南亚国家和地区。已知2件甲种开关与3件乙种开关销售额相同;3件甲种开关比2件乙种开关的销售额多1500元。
(1)甲种开关与乙种开关的销售单价各为多少元?
(2)若甲、乙两种开关的销售总收入不低于5400万元,则至少销售甲种开关多少万件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】王师傅非常喜欢自驾游,为了解他新买的轿车的耗油情况,将油箱加满后进行了耗油实验,得到下表中的数据:
轿车行驶的路程
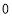
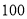
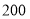
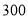
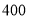
······
油箱中的剩余油量
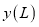
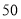
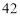
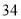
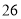
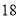
·····
(1)在这个问题中,自变量是_ 因变量是_ ;
(2)该轿车油箱的容量为__ L,行驶
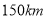 时,估计油箱中的剩余油量为____
时,估计油箱中的剩余油量为____ ;
;(3)王师傅将油箱加满后,驾驶该轿车从
 地前往
地前往 地,到达
地,到达 地时油箱中的剩余油量为
地时油箱中的剩余油量为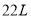 ,请估计
,请估计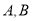 两地之间的距离.
两地之间的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】在《几何原本》中记载着这样的题目:如果同一条线段被两个分点先后分成相等和不相等的线段,以得到的各线段为边作正方形,那么不相等的两个正方形的面积之和等于原线段一半上的正方形与两个分点之间一段上正方形的面积之和的两倍.王老师带领学生在阅读的基础上画出的部分图形如图,已知线段
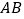 ,点
,点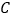 为线段
为线段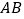 的中点,点
的中点,点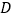 为线段
为线段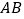 上任意一点(
上任意一点(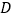 不与
不与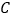 重合),分别以
重合),分别以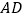 和
和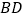 为边在
为边在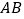 的下方作正方形
的下方作正方形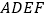 和正方形
和正方形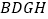 ,以
,以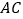 和
和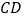 为边在线段下方作正方形
为边在线段下方作正方形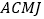 和正方形
和正方形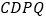 ,则正方形
,则正方形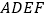 与正方形
与正方形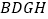 的面积之和等于正方形
的面积之和等于正方形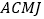 和正方形
和正方形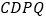 面积之和的两倍.
面积之和的两倍.(1)请你画出正方形
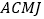 和正方形
和正方形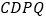 (不必尺规作图);
(不必尺规作图);(2)设
 ,
,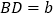 ,根据题意写出关于
,根据题意写出关于 的等式并证明.
的等式并证明.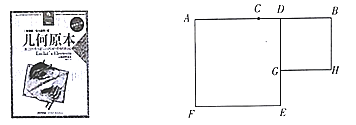
-
科目: 来源: 题型:
查看答案和解析>>【题目】周末,小明乘坐家门口的公交车到和平公园游玩,他先乘坐公交车
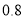 小时后达到书城,逗留一段时间后继续坐公交车到和平公园,小明出发一段时间后,小明的妈妈不放心,于是驾车沿相同的路线前往和平公园.如图是他们离家的路程
小时后达到书城,逗留一段时间后继续坐公交车到和平公园,小明出发一段时间后,小明的妈妈不放心,于是驾车沿相同的路线前往和平公园.如图是他们离家的路程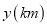 与离家时间
与离家时间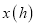 的关系图,请根据图回答下列问题:
的关系图,请根据图回答下列问题: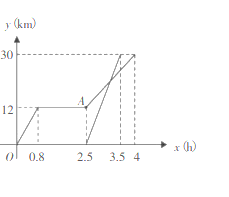
(1)小明家到和平公园的路程为
 ,他在书城逗留的时间为 _
,他在书城逗留的时间为 _ ;
;(2)图中
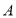 点表示的意义是 ;
点表示的意义是 ;(3)求小明从书城到和平公园的平均速度和小明的妈妈驾车的平均速度(平均速度
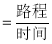 )
) -
科目: 来源: 题型:
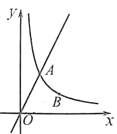
查看答案和解析>>【题目】如图,直线y=2x与反比例函数
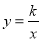 (k≠0,x>0)的图象交于点A(1,m),点B(n,t)是反比例函数图象上一点,且n=2t。
(k≠0,x>0)的图象交于点A(1,m),点B(n,t)是反比例函数图象上一点,且n=2t。(1)求k的值和点B坐标;
(2)若点P在x轴上,使得△PAB的面积为2,直接写出点P坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,正方形ABCD和正方形AEFG,连接DG,BE。
(1)发现
当正方形AEFG绕点A旋转,如图2,①线段DG与BE之间的数量关系是____________。②直线DG与直线BE之间的位置关系是____________。
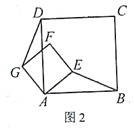
(2)探究
如图3,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE,证明:直线DG⊥BE
(3)应用
在(2)情况下,连结GE(点E在AB上方),若GE∥AB,且AB=
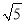 ,AE=1,则线段DG是多少?(直接写出结论)
,AE=1,则线段DG是多少?(直接写出结论)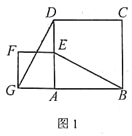
相关试题

