【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论
①abc>0;
②4a+b=0;
③9a+c>3b;
④当x>﹣1时,y的值随x值的增大而增大,其中正确的结论有( )
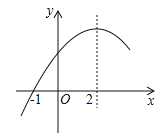
A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】A
【解析】解:①由图象可得c>0.∵x=﹣![]() =2,∴ab<0,∴abc<0,故①错误;
=2,∴ab<0,∴abc<0,故①错误;
②∵抛物线的对称轴为直线x=﹣![]() =2,∴b=﹣4a,即4a+b=0,故本结论正确;
=2,∴b=﹣4a,即4a+b=0,故本结论正确;
③∵当x=﹣3时,y<0,∴9a﹣3b+c<0,即9a+c<3b,故本结论错误;
④∵对称轴为直线x=2,∴当﹣1<x<2时,y的值随x值的增大而增大,当x>2时,y随x的增大而减小,故本结论错误.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一边是另一边的
 倍的三角形叫做智慧三角形,这两边中较长边称为智慧边,这两边的 夹角叫做智慧角.
倍的三角形叫做智慧三角形,这两边中较长边称为智慧边,这两边的 夹角叫做智慧角.(1)在 Rt△ABC 中,∠ACB=90°,若∠A 为智慧角,则∠B 的度数为 ;
(2)如图①,在△ABC 中,∠A=45°,∠B=30°,求证:△ABC 是智慧三角形;
(3)如图②,△ABC 是智慧三角形,BC 为智慧边,∠B 为智慧角,A(3,0),点 B,C 在函数 y=
 (x>0)的图像上,点 C 在点 B 的上方,且点 B 的纵坐标为
(x>0)的图像上,点 C 在点 B 的上方,且点 B 的纵坐标为 .当△ABC是直角三角形时,求 k 的值.
.当△ABC是直角三角形时,求 k 的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】【题目】如图①,一次函数 y=
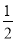 x - 2 的图像交 x 轴于点 A,交 y 轴于点 B,二次函数 y=
x - 2 的图像交 x 轴于点 A,交 y 轴于点 B,二次函数 y=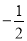 x2 bx c的图像经过 A、B 两点,与 x 轴交于另一点 C.
x2 bx c的图像经过 A、B 两点,与 x 轴交于另一点 C.(1)求二次函数的关系式及点 C 的坐标;
(2)如图②,若点 P 是直线 AB 上方的抛物线上一点,过点 P 作 PD∥x 轴交 AB 于点 D,PE∥y 轴交 AB 于点 E,求 PD+PE 的最大值;
(3)如图③,若点 M 在抛物线的对称轴上,且∠AMB=∠ACB,求出所有满足条件的点 M的坐标.
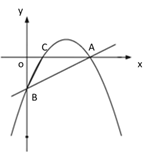
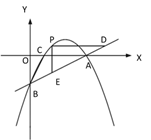
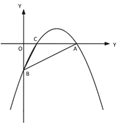
① ② ③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上
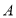 点表示数
点表示数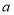 ,
,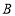 点表示数
点表示数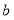 ,
,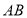 表示
表示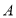 点和
点和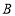 点之间的距离,且
点之间的距离,且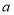 ,
,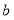 满足
满足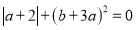 .
.
(1)求
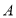 ,
,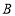 两点之间的距离;
两点之间的距离;(2)若在数轴上存在一点
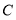 ,且
,且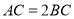 ,直接写出
,直接写出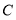 点表示的数;
点表示的数;(3)若在原点
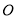 处放一挡板,一小球甲从点
处放一挡板,一小球甲从点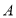 处以1个单位/秒的速度向左运动;同时另一小球乙从点
处以1个单位/秒的速度向左运动;同时另一小球乙从点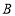 处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),
处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),
①分别表示甲、乙两小球到原点的距离(用t表示);
②求甲、乙两小球到原点的距离相等时经历的时间. -
科目: 来源: 题型:
查看答案和解析>>【题目】下图是某同学在沙滩上用石于摆成的小房子,第一个图形由5个小石子组成,第二个图形由12个小石子组成,第三个图形由21个小石子组成,,观察图形的变化规律,第8个小房子用的小石子数量是( )

A.78B.96C.105D.108
-
科目: 来源: 题型:
查看答案和解析>>【题目】某天上午出租车司机小张在东西走向的大街上营运,如果规定向东为正,向西为负,他这天上午所接送六位乘客的行驶里程(单位:km)如下表:(等待乘客时,空车里程忽略不计)
乘客顺序
第一位
第二位
第三位
第四位
第五位
第六位
行驶里程
-2
+8
-1
+1
-9
-2
(1)将最后一位乘客送到目的地时,小张在出发地什么位置?
(2)若汽车耗油量为0.06
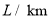 ,这天上午小张接送乘客,出租车共耗油多少升?
,这天上午小张接送乘客,出租车共耗油多少升?(3)若出租车起步价为5元,起步里程为3km(包括3km),超过部分1.2元/km,问小张这天上午共收车费多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】福建省教育厅日前发布文件,从2019年开始,体育成绩将按一定的原始分计入中考总分。某校为适应新的中考要求,决定为体育组添置一批体育器材。学校准备在网上订购一批某品牌足球和跳绳,在查阅天猫网店后发现足球每个定价150元,跳绳每条定价30元.现有A、B两家网店均提供包邮服务,并提出了各自的优惠方案.
A网店:买一个足球送一条跳绳;
B网店:足球和跳绳都按定价的90%付款.
已知要购买足球40个,跳绳x条(x>40)
(1)若在A网店购买,需付款 元(用含x的代数式表示).
若在B网店购买,需付款 元(用含x的代数式表示).
(2)若x=100时,通过计算说明此时在哪家网店购买较为合算?
(3)当x=100时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法,
并计算需付款多少元?
相关试题

