【题目】有一边是另一边的![]() 倍的三角形叫做智慧三角形,这两边中较长边称为智慧边,这两边的 夹角叫做智慧角.
倍的三角形叫做智慧三角形,这两边中较长边称为智慧边,这两边的 夹角叫做智慧角.
(1)在 Rt△ABC 中,∠ACB=90°,若∠A 为智慧角,则∠B 的度数为 ;
(2)如图①,在△ABC 中,∠A=45°,∠B=30°,求证:△ABC 是智慧三角形;
(3)如图②,△ABC 是智慧三角形,BC 为智慧边,∠B 为智慧角,A(3,0),点 B,C 在函数 y=![]() (x>0)的图像上,点 C 在点 B 的上方,且点 B 的纵坐标为
(x>0)的图像上,点 C 在点 B 的上方,且点 B 的纵坐标为![]() .当△ABC是直角三角形时,求 k 的值.
.当△ABC是直角三角形时,求 k 的值.


参考答案:
【答案】(1)45°.(2)见解析;(3)k=4![]() 或18+15
或18+15![]() .
.
【解析】试题分析:(1)由智慧角的定义得到AB=![]() AC,解直角三角形即可得到结论.
AC,解直角三角形即可得到结论.
(2)过点C作CD⊥AB于点D.在Rt△ACD中,由∠A=45°,得到AC=![]() DC.
DC.
在Rt△BCD中,由∠B=30°,得到BC=2DC,即可得到结论.
(3)分两种情况讨论:①∠ABC=90°;②∠BAC=90°.
试题解析:解:(1)∵∠ACB=90°,若∠A 为智慧角,∴AB=![]() AC,∴cosA=
AC,∴cosA=![]() ,∴∠A=45°,∴∠B=45°.
,∴∠A=45°,∴∠B=45°.
(2)如图1,过点C作CD⊥AB于点D.
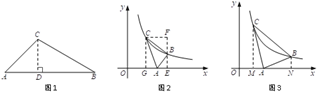
在Rt△ACD中,∠A=45°,∴AC=![]() DC.
DC.
在Rt△BCD中,∠B=30°,∴BC=2DC,∴![]() =
=![]() ,∴△ABC是智慧三角形.
,∴△ABC是智慧三角形.
(3)由题意可知:∠ABC=90°或∠BAC=90°.
①当∠ABC=90°时,如图2,过点B作BE⊥x轴于点E,过点C作CF⊥EB交EB延长线于点F,过点C作CG⊥x轴于点G,则∠AEB=∠F=∠ABC=90°,∴∠BCF+∠CBF=∠ABE+∠CBF=90°,∴∠BCF=∠ABE,∴△BCF∽△ABE,∴![]() =
=![]() =
=![]() =
=![]() .
.
设AE=a,则BF=![]() a.∵BE=
a.∵BE=![]() ,∴CF=2.
,∴CF=2.
∵OG=OA+AE-GE=3+a-2=1+a,CG=EF=![]() +
+![]() a,∴B(3+a,
a,∴B(3+a, ![]() ),C(1+a,
),C(1+a, ![]() +
+![]() a).∵点B,C在函数y=
a).∵点B,C在函数y=![]() (x>0)的图像上,∴
(x>0)的图像上,∴![]() (3+a)=(1+a)(
(3+a)=(1+a)( ![]() +
+![]() a)=k.
a)=k.
解得:a1=1,a2=-2(舍去),∴k=![]() .
.
②当∠BAC=90°时,如图3,过点C作CM⊥x轴于点M,过点B作BN⊥x轴于点N,则∠CMA=∠CAB=∠ANB=90°,∴∠MCA+∠CAM=∠BAN+∠CAM=90°,∴∠MCA=∠BAN.由(1)知∠B=45°,∴△ABC是等腰直角三角形,∴AC=AB.
由①知△MAC∽△NBA,∴△MAC≌△NBA(AAS),∴AM=BN=![]() .
.
设CM=AN=b,则ON=3+b,∴B(3+b, ![]() ),C(3-
),C(3-![]() ,b).
,b).
∵点B,C在函数y=![]() (x>0)的图像上,∴
(x>0)的图像上,∴![]() (3+b)=(3-
(3+b)=(3-![]() )b=k,
)b=k,
解得:b=9![]() +12,∴k=18+15
+12,∴k=18+15![]() .
.
综上所述:k=4![]() 或18+15
或18+15![]() .
.
-
科目: 来源: 题型:
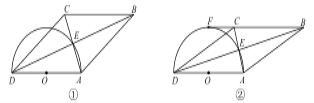
查看答案和解析>>【题目】四边形 ABCD 的对角线交于点 E,且 AE=EC,BE=ED,以 AD 为直径的半圆过点 E,圆心 为 O.
(1)如图①,求证:四边形 ABCD 为菱形;
(2)如图②,若 BC 的延长线与半圆相切于点 F,且直径 AD=6,求弧AE 的长.
-
科目: 来源: 题型:
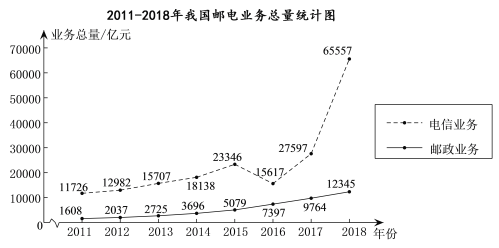
查看答案和解析>>【题目】下面的统计图反映了我国邮电业务(含邮政业务与电信业务)总量的情况.
(以上数据来源于国家统计局)
根据统计图提供的信息,下列有关我国邮电业务总量推断不合理的是( )
A. 2018年,电信业务总量比邮政业务总量的5倍还多
B. 2011—2018年,邮政业务总量与电信业务总量都是逐年增长的
C. 与2017年相比,2018年邮政业务总量的增长率超过20%
D. 2011—2018年,电信业务总量年增长的平均值大于邮政业务总量年增长的平均值
-
科目: 来源: 题型:
查看答案和解析>>【题目】菱形
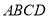 中,
中,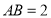 ,
,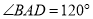 ,则菱形
,则菱形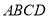 的面积为_____________.
的面积为_____________. -
科目: 来源: 题型:
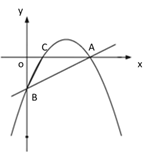
查看答案和解析>>【题目】【题目】如图①,一次函数 y=
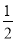 x - 2 的图像交 x 轴于点 A,交 y 轴于点 B,二次函数 y=
x - 2 的图像交 x 轴于点 A,交 y 轴于点 B,二次函数 y=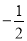 x2 bx c的图像经过 A、B 两点,与 x 轴交于另一点 C.
x2 bx c的图像经过 A、B 两点,与 x 轴交于另一点 C.(1)求二次函数的关系式及点 C 的坐标;
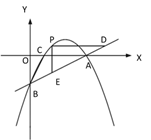
(2)如图②,若点 P 是直线 AB 上方的抛物线上一点,过点 P 作 PD∥x 轴交 AB 于点 D,PE∥y 轴交 AB 于点 E,求 PD+PE 的最大值;
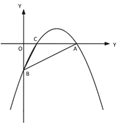
(3)如图③,若点 M 在抛物线的对称轴上,且∠AMB=∠ACB,求出所有满足条件的点 M的坐标.
① ② ③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上
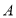 点表示数
点表示数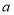 ,
,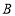 点表示数
点表示数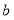 ,
,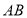 表示
表示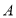 点和
点和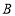 点之间的距离,且
点之间的距离,且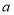 ,
,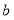 满足
满足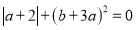 .
.
(1)求
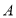 ,
,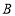 两点之间的距离;
两点之间的距离;(2)若在数轴上存在一点
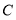 ,且
,且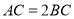 ,直接写出
,直接写出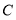 点表示的数;
点表示的数;(3)若在原点
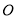 处放一挡板,一小球甲从点
处放一挡板,一小球甲从点 处以1个单位/秒的速度向左运动;同时另一小球乙从点
处以1个单位/秒的速度向左运动;同时另一小球乙从点 处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),
处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),
①分别表示甲、乙两小球到原点的距离(用t表示);
②求甲、乙两小球到原点的距离相等时经历的时间. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论
①abc>0;
②4a+b=0;
③9a+c>3b;
④当x>﹣1时,y的值随x值的增大而增大,其中正确的结论有( )
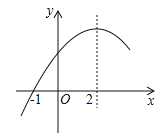
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

