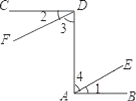
【题目】已知:如图,CD⊥DA,DA⊥AB,∠1=∠2.试确定射线DF与AE的位置关系,并说明你的理由.
某同学在解决上面问题时,准备三步走,请你完成他的步骤.
(1)问题的结论:DF____AE.
(2)思路要使DF_____AE,只要∠3=____.
(3)说理过程:
解:∵CD⊥DA,DA⊥AB,
∴∠CDA=∠DAB=________.( )
又∵∠1=∠2,
∴∠CDA﹣∠2=____﹣____,( )
即∠3=______,
∴DF_____AE.( )
参考答案:
【答案】∥;∥,∠4;90°,垂直定义,∠DAB,∠1,等式的性质,∠4,∥,内错角相等,两直线平行.
【解析】
根据已知条件、以及平行线的判定进行填空即可.
解:(1)问题的结论:DF∥AE.
(2)思路要使DF∥AE,只要∠3=∠4.
(3)说理过程:
解:∵CD⊥DA,DA⊥AB,
∴∠CDA=∠DAB=90°.( 垂直定义)
又∵∠1=∠2,
∴∠CDA-∠2=∠BAD-∠1,( 等式的性质)
即∠3=∠4,
∴DF∥AE.( 内错角相等,两直线平行).
故答案为:∥;∥,∠4;90°,垂直定义,∠DAB,∠1,等式的性质,∠4,∥,内错角相等,两直线平行.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形
 中,
中, ,
, ,
, .
.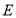 是边
是边 的中点,联结
的中点,联结 、
、 ,且
,且 .设
.设 ,
, .
.

(1)如果
 ,求
,求 的长;
的长;(2)求
 关于
关于 的函数解析式,并写出自变量
的函数解析式,并写出自变量 的取值范围;
的取值范围;(3)联结
 .如果
.如果 是以边
是以边 为腰的等腰三角形,求
为腰的等腰三角形,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的内接正五边形ABCDE的对角线AD与BE相交于点G,AE=2,则EG的长是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,AB=AC,D,E是斜边BC上两点,且∠DAE=45°,将△ABE绕点A顺时针旋转90°后,得到△ACF,连接DF,则下列结论中有( )个是正确的。
①∠DAF=45° ②△ABE≌△ACD ③AD平分∠EDF ④


A. 4B. 3C. 2D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,连接BD,且BD=CD,过点A作AM⊥BD于点M,过点D作DN⊥AB于点N,且DN=
 ,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=_____.
,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,BC=8,AC=6,将△ABC沿AE折叠 使点C恰好落在AB边上的点F处.求BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学活动课上,张老师说:“
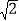 是无理数,无理数就是无限不循环小数,同学们,你能把
是无理数,无理数就是无限不循环小数,同学们,你能把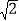 的小数部分全部写出来吗?”大家议论纷纷,晶晶同学说:“要把它的小数部分全部写出来是非常难的,但我们可以用(
的小数部分全部写出来吗?”大家议论纷纷,晶晶同学说:“要把它的小数部分全部写出来是非常难的,但我们可以用(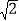 ﹣1)表示它的小数部分.”张老师说:“晶晶同学的说法是正确的,因为1<2<4,所以1<
﹣1)表示它的小数部分.”张老师说:“晶晶同学的说法是正确的,因为1<2<4,所以1<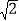 <2,所以
<2,所以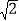 的整数部分是1,将这个数减去其整数部分,差就是小数部分.”亮亮说:“既然如此,因为2<
的整数部分是1,将这个数减去其整数部分,差就是小数部分.”亮亮说:“既然如此,因为2<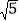 <3,所以
<3,所以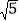 的小数部分就是(
的小数部分就是(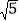 ﹣2)了.”张老师说:“亮亮真的很聪明.”接着,张老师出示了一道练习题:“已知8+
﹣2)了.”张老师说:“亮亮真的很聪明.”接着,张老师出示了一道练习题:“已知8+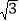 =x+y,其中x是一个整数,且0<y<1,请你求出2x+(
=x+y,其中x是一个整数,且0<y<1,请你求出2x+(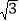 ﹣y)2019的值”.请同样聪明的你给出正确答案.
﹣y)2019的值”.请同样聪明的你给出正确答案.
相关试题

