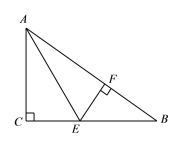
【题目】如图,在Rt△ABC中,∠C=90°,BC=8,AC=6,将△ABC沿AE折叠 使点C恰好落在AB边上的点F处.求BE的长.
参考答案:
【答案】BE=5
【解析】
根据折叠性质可知CE=EF,EF⊥AB,利用勾股定理可求出AB的长,进而可知BF的长,在RtBEF中,BE=BC-CE=BC-EF,设BE=x,则EF=8-x,利用勾股定理列方程即可求出BE的长.
∵将△ABC沿AE折叠 使点C恰好落在AB边上的点F,
∴AC=AF=6,EF⊥AB,CE=EF,
∵在Rt△ABC中,∠C=90°,BC=8,AC=6,
∴AB=![]() =10,
=10,
∴BF=10-6=4,
设BE=x,则EF=8-x,
∴x2=(x-8)2+42,
解方程得:x=5.即BE=5.
-
科目: 来源: 题型:
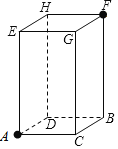
查看答案和解析>>【题目】已知长方体的长为1cm、宽为1cm、高为4cm(其中AC=1cm,BC=1cm,CG=4cm).一只蚂蚁如果沿长方体的表面从A点爬到F点,最短的路程是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=﹣x2+2x+m.
(1)如果二次函数的图象与x轴有两个交点,求m的取值范围;
(2)如图,二次函数的图象过点A(3,0),与y轴交于点B,直线AB与这个二次函数图象的对称轴交于点P,求点P的坐标.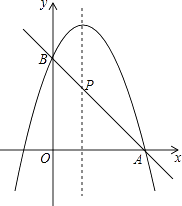
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店经营儿童玩具,已知成批购进时的单价是20元.调查发现:销售单价是30元时,月销售量是200件,而销售单价每上涨2元,月销售量就减少10件,但每件玩具售价不能高于40元.设每件玩具的销售单价上涨了x元时,月销售利润为y元.
(1)求y与x的函数关系式并直接写出自变量x的取值范围.
(2)每件玩具的售价定为多少元时,月销售利润恰为2280元?
(3)每件玩具的售价定为多少元时,月销售利润达到最大?最大为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,平面直角坐标系中,等腰直角三角形的直角边BC在x轴正半轴上滑动,点C的坐标为(t,0),直角边AC=4,经过O,C两点做抛物线y1=ax(x﹣t)(a为常数,a>0),该抛物线与斜边AB交于点E,直线OA:y2=kx(k为常数,k>0)
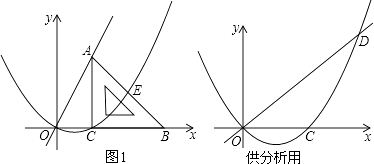
(1)填空:用含t的代数式表示点A的坐标及k的值:A , k=;
(2)随着三角板的滑动,当a= 时:
时:
①请你验证:抛物线y1=ax(x﹣t)的顶点在函数y=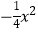 的图象上;
的图象上;
②当三角板滑至点E为AB的中点时,求t的值;
(3)直线OA与抛物线的另一个交点为点D,当t≤x≤t+4,|y2﹣y1|的值随x的增大而减小,当x≥t+4时,|y2﹣y1|的值随x的增大而增大,求a与t的关系式及t的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=45,∠AOB内有一定点P,且OP=10.在OA上有一动点Q,OB上有一动点R.若ΔPQR周长最小,则最小周长是()

A. 10 B.
 C. 20 D.
C. 20 D. 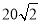
-
科目: 来源: 题型:
查看答案和解析>>【题目】将△ABC绕O点顺时针旋转50°得△A1B1C1(A、B分别对应A1、B1),则直线AB与直线A1B1的夹角(锐角)为( )
A.130°
B.50°
C.40°
D.60°
相关试题

