搜索
【题目】若直线y＝kx＋b的大致图象如图所示，则不等式kx＋b 
3的解集是（ ）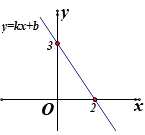
A.x ＞0
B. x ＜2
C.x ≥0
D.x≤2
参考答案：
【答案】C
【解析】解：从图上可以看出函数过两个点（0，3）和（2，0）
则一次函数的解析式为：y=- 
x+3.
依据题意有- x+3≤3
x≥0
所以答案是C
【考点精析】认真审题，首先需要了解一次函数的性质(一般地，一次函数y=kx+b有下列性质：（1）当k>0时，y随x的增大而增大（2）当k<0时，y随x的增大而减小)，还要掌握一次函数的图象和性质(一次函数是直线，图像经过仨象限；正比例函数更简单,经过原点一直线；两个系数k与b,作用之大莫小看，k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减；k为负来左下展,变化规律正相反；k的绝对值越大,线离横轴就越远)的相关知识才是答题的关键．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，抛物线y＝mx2－2mx＋m－1(m＞0)与x轴的交点为A，B，顶点为C，将抛物线在A，C，B之间的部分记为图象E(A，B两点除外)．
（1）求抛物线的顶点坐标．
（2）AB＝6时，经过点C的直线y＝kx＋b(k≠0)与图象E有两个交点，结合函数的图象，求k的取值范围．
（3）若横、纵坐标都是整数的点叫整点．
①当m＝1时，求线段AB上整点的个数；
②若抛物线在点A，C，B之间的图象E与线段AB所围成的区域内(包括边界)恰有6个整点，结合函数的图象，求m的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】某班将买一些乒乓球和乒乓球拍．了解信息如下：甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍．乒乓球拍每副定价30元，乒乓球每盒定价5元；经洽谈：甲店每买一副球拍赠一盒乒乓球；乙店全部按定价的9折优惠．该班需球拍5副，乒乓球若干盒(不小于5盒)．问：
(1)当购买乒乓球x盒时，两种优惠办法各应付款多少元？(用含x的代数式表示)
(2)如果要购买15盒乒乓球时，请你去办这件事，你打算去哪家商店购买？为什么？
-
科目： 来源： 题型：
查看答案和解析>>【题目】下表记录的是流花河今年某一周内的水位变化情况，上周末（星期六）的水位已达到警戒水位
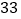米．（正号表示水位比前一天上升，负号表示水位比前一天下降）星期
日
一
二
三
四
五
六
水位变化
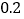
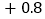
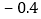
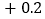
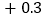
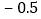
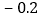
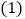本周哪一天河流的水位最高？哪一天河流的水位最低？它们位于警戒水位之上还是之下？
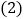与上周末相比，本周末河流的水位是上升了还是下降了？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD中，点E、F分别是BC、CD上的动点（不与点B，C，D重合），且∠EAF=45°，AE、AF与对角线BD分别相交于点G、H,连接EH、EF,则下列结论：① △ABH∽△GAH; ② △ABG∽△HEG; ③ AE=
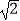AH; ④ EH⊥AF; ⑤ EF=BE+DF
其中正确的有（ ）个。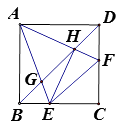
A.2
B.3
C.4
D.5 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在直角坐标系中，矩形OABC的顶点A在x轴上，顶点C在y轴上，B（4，3），连接OB，将△OAB沿直线OB翻折，得△ODB,OD与BC相交于点E,若双曲线
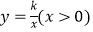经过点E,则k= ;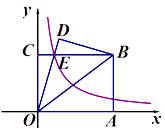
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在梯形纸片ABCD中，AD//BC，AD>CD，将纸片沿过点D的直线折叠，使点C落在AD上的点C处，折痕DE交BC于点E，连结C′E．
求证：四边形CDC′E是菱形．
相关试题
