【题目】在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-1(m>0)与x轴的交点为A,B,顶点为C,将抛物线在A,C,B之间的部分记为图象E(A,B两点除外).
(1)求抛物线的顶点坐标.
(2)AB=6时,经过点C的直线y=kx+b(k≠0)与图象E有两个交点,结合函数的图象,求k的取值范围.
(3)若横、纵坐标都是整数的点叫整点.
①当m=1时,求线段AB上整点的个数;
②若抛物线在点A,C,B之间的图象E与线段AB所围成的区域内(包括边界)恰有6个整点,结合函数的图象,求m的取值范围.
参考答案:
【答案】
(1)
C(1,-1).
(2)
AB=6时,抛物线与x轴的两个交点分别是(-2,0),(4,0),又因为顶点为(-1,1),当直线经过C与A,C与B时,分别解得k= ![]() ,所以k的取值范围为
,所以k的取值范围为 ![]() <k<0,或0<k<
<k<0,或0<k< ![]() .
.
(3)
①当m=1时,抛物线表达式为y=x2-2x,因此A、B的坐标分别为(0,0)和(2,0),则线段AB上的整点有(0,0),(1,0),(2,0)共3个.
②抛物线顶点为(1,-1),则指定区域的整点的纵坐标只能为-1或者0,所以即要求AB线段上(含AB两点)必须有5个整点;
令y=mx2-2mx+m-1=0,得到A、B两点坐标分别为( ![]() ,0),(
,0),( ![]() ,0),即5个整点是以(1,0)为中心向两侧分散,
,0),即5个整点是以(1,0)为中心向两侧分散,
进而得到2≤ ![]() <3,所以
<3,所以 ![]() <m≤
<m≤ ![]() .
.
【解析】(1)y=mx2-2mx+m-1=m(x-1)2-1,
则顶点C(1,-1).
(2)因为y=mx2-2mx+m-1=m(x-1)2-1,
所以对称轴为直线x=1,
因为AB=6,所以抛物线与x轴的两个交点分别是(-2,0),(4,0),
因为直线y=kx+b(k≠0)过C(1,-1)点,则y=kx-k-1,
当直线经过(-2,0)时,代入得-2k-k-1=0,
解得k=![]() ;
;
当直线经过(4,0)时,代入得4k-k-1=0,
解得k=![]() .
.
综上所述,因为图象E不包括A,B,则![]() <k<0,或0<k<
<k<0,或0<k< ![]() .
.
(3)①当m=1时,抛物线表达式为y=x2-2x,
因此A、B的坐标分别为(0,0)和(2,0),
则线段AB上的整点有(0,0),(1,0),(2,0)共3个.
②抛物线顶点为(1,-1),
则指定区域的整点的纵坐标只能为-1或者0,
所以即要求AB线段上(含AB两点)必须有5个整点;
令y=mx2-2mx+m-1=0,得到A、B两点坐标分别为( ![]() ,0),(
,0),( ![]() ,0),即5个整点是以(1,0)为中心向两侧分散,分别为(-1,0),(0,0),(1,0),(2,0),(3,0),
,0),即5个整点是以(1,0)为中心向两侧分散,分别为(-1,0),(0,0),(1,0),(2,0),(3,0),
则-2<![]() ≤-1,
≤-1,
进而得到2≤ ![]() <3,
<3,
所以 ![]() <m≤
<m≤ ![]() .
.
(1)根据顶点公式(![]() ),代入相应值计算即可或者配成顶点式;
),代入相应值计算即可或者配成顶点式;
(2)图象E指的是A,B,C之间所构成的图象,根据C(1.-1)可求出b,根据与图象E有两个交点可求出k的聚值范围;要理解当k>0时,随着k的增大,直线与x轴的正半轴的较小的夹角会越来越大;当k<0时,随着k的增大,直线与x轴的正半轴的较小的夹角会越来越小;
(3)①根据m的值可求出A,B的坐标,即可得到线段AB的整点坐标,包括A点和B点;
②因为二次函数的最小值是-1,而在抛物线在点A,C,B之间的图象E与线段AB所围成的区域内(包括边界)中是-1≤y<0的,除了(1,-1),所以其他整点一定在线段AB上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标平面中,O为原点,点A的坐标为(20,0),点B在第一象限内,BO=10,sin∠BOA=
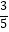 .
.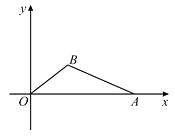
(1)在图中,求作△ABO的外接圆;(尺规作图,不写作法但需保留作图痕迹)
(2)求点B的坐标与cos∠BAO的值;
(3)若A,O位置不变,将点B沿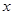 轴正半轴方向平移使得△ABO为等腰三角形,请直接写出平移距离.
轴正半轴方向平移使得△ABO为等腰三角形,请直接写出平移距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,猜想四边形ADCE的形状,并给予证明.
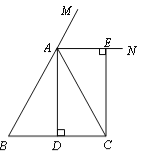
-
科目: 来源: 题型:
查看答案和解析>>【题目】在已知线段AB的同侧构造∠FAB=∠GBA,并且在射线AF,BG上分别取点D和E,在线段AB上取点C,连结DC和EC.
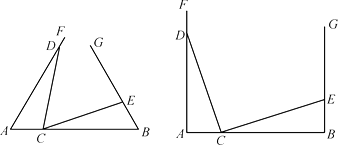
Ⅰ、如图,若AD=3,BE=1,△ADC≌△BCE.在∠FAB=∠GBA=60或∠FAB=∠GBA=90两种情况中任选一种,解决以下问题:
①线段AB的长度是否发生变化,直接写出长度或变化范围;
②∠DCE的度数是否发生变化,直接写出度数或变化范围.
Ⅱ、若AD=a,BE=b,∠FAB=∠GBA=α,且△ADC和△BCE这两个三角形全等,请求出:
①线段AB的长度或取值范围,并说明理由;
②∠DCE的度数或取值范围,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某班将买一些乒乓球和乒乓球拍.了解信息如下:甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍.乒乓球拍每副定价30元,乒乓球每盒定价5元;经洽谈:甲店每买一副球拍赠一盒乒乓球;乙店全部按定价的9折优惠.该班需球拍5副,乒乓球若干盒(不小于5盒).问:
(1)当购买乒乓球x盒时,两种优惠办法各应付款多少元?(用含x的代数式表示)
(2)如果要购买15盒乒乓球时,请你去办这件事,你打算去哪家商店购买?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表记录的是流花河今年某一周内的水位变化情况,上周末(星期六)的水位已达到警戒水位
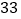 米.(正号表示水位比前一天上升,负号表示水位比前一天下降)
米.(正号表示水位比前一天上升,负号表示水位比前一天下降)星期
日
一
二
三
四
五
六
水位变化
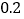
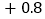
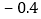
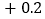
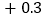
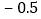
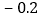
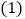 本周哪一天河流的水位最高?哪一天河流的水位最低?它们位于警戒水位之上还是之下?
本周哪一天河流的水位最高?哪一天河流的水位最低?它们位于警戒水位之上还是之下?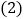 与上周末相比,本周末河流的水位是上升了还是下降了?
与上周末相比,本周末河流的水位是上升了还是下降了? -
科目: 来源: 题型:
查看答案和解析>>【题目】若直线y=kx+b的大致图象如图所示,则不等式kx+b
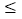 3的解集是( )
3的解集是( )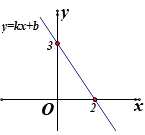
A.x >0
B. x <2
C.x ≥0
D.x≤2
相关试题

