【题目】如图,正方形ABCD中,点E、F分别是BC、CD上的动点(不与点B,C,D重合),且∠EAF=45°,AE、AF与对角线BD分别相交于点G、H,连接EH、EF,则下列结论:① △ABH∽△GAH; ② △ABG∽△HEG; ③ AE= ![]() AH; ④ EH⊥AF; ⑤ EF=BE+DF
AH; ④ EH⊥AF; ⑤ EF=BE+DF
其中正确的有( )个。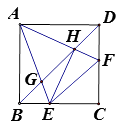
A.2
B.3
C.4
D.5
参考答案:
【答案】D
【解析】①BD是正方形ABCD的对角线,所以∠ABD=45°,
∵∠EAF=45°,∴∠ABD=∠EAF=45°.
∵∠AHB=∠AHG,∴ ![]() ABH∽
ABH∽ ![]() GAH,即①正确。
GAH,即①正确。
②四边形ABCD是正方形,BD为其对角线,所以∠DBC=45°.
∵∠EAF=45°,∴∠EAF=∠DBC.
∴ ![]() AGD∽
AGD∽ ![]() BGE,
BGE, ![]() ,即
,即 ![]()
∵∠AGB=∠HE,∴△ABG∽△HEG.
故②正确.
③由②知△ABG∽△HEG,则∠ABG=∠AEH.
易知∠ABG=45°,所以∠AEH=45°.
∵∠EAH=45°,∴ ![]() AEH是等腰直角三角形.
AEH是等腰直角三角形.
∴ ![]() =
= ![]() ,AE=
,AE= ![]() AH
AH
即③正确.
④由③知 ![]() AEH是等腰直角三角形,所以EH⊥AF,即④正确。
AEH是等腰直角三角形,所以EH⊥AF,即④正确。
⑤将△ADF绕点A顺时针旋转90°得到△ABM.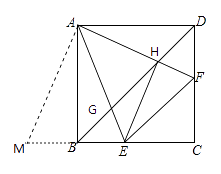
易知BM=DF,∠DAF=∠BAM,AF=AM
四边形ABCD为正方形,∠EAF=45°,则∠BAE+∠DAF=45°
即∠BAM+∠BAE=∠MAE=45°.
∵AE=AE
∴ ![]() AFE≌
AFE≌ ![]() AME,ME=EF.
AME,ME=EF.
∵ME=MB+BE=DF+BE
∴EF=BE+DF。
所以五个命题都是正确,答案为D.
根据相似三角形的判定,证明三角形相似。对于最后一问,注意问题的转化,通过作辅助线,证明ME=EF=EB+DF。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班将买一些乒乓球和乒乓球拍.了解信息如下:甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍.乒乓球拍每副定价30元,乒乓球每盒定价5元;经洽谈:甲店每买一副球拍赠一盒乒乓球;乙店全部按定价的9折优惠.该班需球拍5副,乒乓球若干盒(不小于5盒).问:
(1)当购买乒乓球x盒时,两种优惠办法各应付款多少元?(用含x的代数式表示)
(2)如果要购买15盒乒乓球时,请你去办这件事,你打算去哪家商店购买?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表记录的是流花河今年某一周内的水位变化情况,上周末(星期六)的水位已达到警戒水位
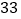 米.(正号表示水位比前一天上升,负号表示水位比前一天下降)
米.(正号表示水位比前一天上升,负号表示水位比前一天下降)星期
日
一
二
三
四
五
六
水位变化
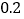
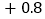
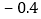
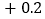
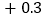
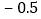
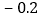
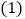 本周哪一天河流的水位最高?哪一天河流的水位最低?它们位于警戒水位之上还是之下?
本周哪一天河流的水位最高?哪一天河流的水位最低?它们位于警戒水位之上还是之下?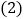 与上周末相比,本周末河流的水位是上升了还是下降了?
与上周末相比,本周末河流的水位是上升了还是下降了? -
科目: 来源: 题型:
查看答案和解析>>【题目】若直线y=kx+b的大致图象如图所示,则不等式kx+b
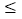 3的解集是( )
3的解集是( )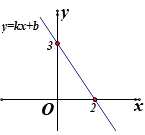
A.x >0
B. x <2
C.x ≥0
D.x≤2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,矩形OABC的顶点A在x轴上,顶点C在y轴上,B(4,3),连接OB,将△OAB沿直线OB翻折,得△ODB,OD与BC相交于点E,若双曲线
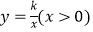 经过点E,则k= ;
经过点E,则k= ;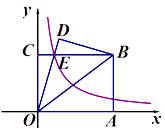
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形纸片ABCD中,AD//BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C处,折痕DE交BC于点E,连结C′E.
求证:四边形CDC′E是菱形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】学生每天锻炼一小时,某校开展了形式多样的体育活动项目,小明对某班同学参加锻炼的情况进行了统计,并绘制了下面的频率统计表和频数分布直方图.请你根据图表信息完成下列各题:
运动项目
频数(人数)
频率
篮球
20
0.40
乒乓球
n
0.10
足球
10
m
其他
15
0.30
合计
a
1.00
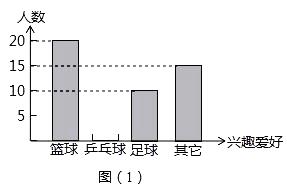
(1)填空: a=;m=;n=;
(2)请将条形统计图补充完整;
(3)该校共有学生1500人,估计参加乒乓球项目的学生有人;
相关试题

