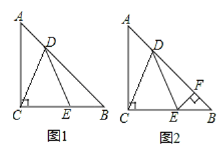
【题目】△ABC中,AC=BC,∠ACB=90°,点D在AB上,E在BC上,且AD=BE,BD=AC.
(1)如图1,求证:DC=DE;
(2)如图2,过E作EF⊥AB于F,若BF=2,求CE的长.
参考答案:
【答案】(1)见解析;(2)4
【解析】
(1)根据SAS证明△ACD≌△BDE,再根据全等三角形的性质即可得DC=DE, 即为所求;
(2)过D作DG⊥CE于G, 过E作EF⊥AB于F,根据等腰直角三角形的性质求出EF的长,根据题意求出∠EDG=∠EDF,根据角平分线的性质求出EG=EF,根据等腰三角形的性质得到答案.
(1)证明:∵AC=BC,∠ACB=90°
∴∠A=∠B=45°
在△ACD和△BDE中

∴△ACD≌△BDE(SAS)
∴DC=DE
(2)解:∵△ACD≌△BDE
∴∠ACD=∠BDE
∵AC=BC,∠B=45°
∴∠BCD=∠BDC=67.5°
∴∠ACD=∠BDE=22.5°
∠CDE=45°
过D作DG⊥CE于G
∵DC=DE
∴∠CDG=∠EDG=22.5°,CG=EG
∴∠CDG=∠EDG=∠EDF =22.5°
∵DG⊥BC,EF⊥AB,∠B=45°
∴FE=EG=GC=FB=2
∴CE=2FB=4

-
科目: 来源: 题型:
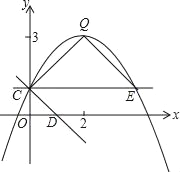
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,且OD=OC.
(1)求直线CD的解析式;
(2)求抛物线的解析式;
(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,求证:△CEQ∽△CDO;
(4)在(3)的条件下,若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
-
科目: 来源: 题型:
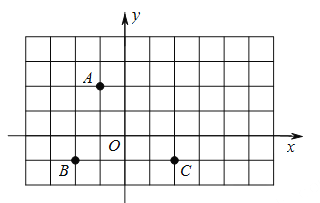
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,点A,B,C均在格点上.
(1)请值接写出点A,B,C的坐标.
(2)若平移线段AB,使B移动到C的位置,请在图中画出A移动后的位置D,依次连接B,C,D,A,并求出四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“数学运算”是数学学科核心素养之一,某校对七年级学生“数学运算能力”情况进行调研,从该校360名七年级学生中抽取了部分学生进行运算能力测试井进行分析,成绩分为A、B、C三个层次,绘制了频数分布表(如下),请根据图表信息解答下列问题:

(1)补全频数分布;
(2)如果成绩为A等级的同学属于优秀,请你估计该校七年级约有多少人达到优秀水平?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,D是等边△ABC外一点,且AD=AC,连接BD,∠CAD的角平分交BD于E.
(1)求证:∠ABD=∠D;
(2)求∠AEB的度数;
(3)△ABC 的中线AF交BD于G(如图2),若BG=DE,求
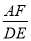 的值.
的值.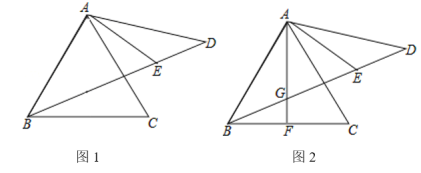
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形
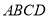 中,对角线
中,对角线 相交于点
相交于点 是对角线
是对角线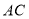 上的两点,给出下列四个条件:①
上的两点,给出下列四个条件:①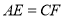 ;②
;②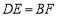 ;③
;③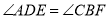 ;④
;④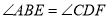 .其中能判定四边形
.其中能判定四边形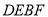 是平行四边形的有( )
是平行四边形的有( )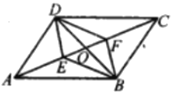
A.①B.①④C.①③④D.①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业前年按可回收垃圾处理费15元/吨、不可回收垃圾处理费25元/吨的收费标准,共支付两种垃圾处理费5000元,从去年元月起,收费标准上调为:可回收垃圾处理费30元/吨,不可回收垃圾处理费100元/吨.若该企业去年处理的这两种垃圾数量与前年相比没有变化,但调价后就要多支付处理费9000元.
(1)该企业前年处理的可回收垃圾和不可回收垃圾各多少吨?
(2)该企业计划今年将上述两种垃圾处理总量减少到200吨,且可回收垃圾不少于不可回收垃圾处理量的3倍,则今年该企业至少有多少吨可回收垃圾?
相关试题

