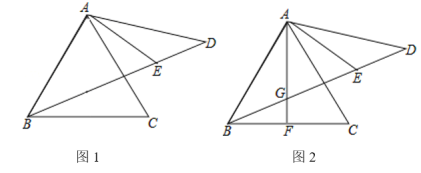
【题目】如图1,D是等边△ABC外一点,且AD=AC,连接BD,∠CAD的角平分交BD于E.
(1)求证:∠ABD=∠D;
(2)求∠AEB的度数;
(3)△ABC 的中线AF交BD于G(如图2),若BG=DE,求![]() 的值.
的值.
参考答案:
【答案】(1)见解析;(2)60°;(3)![]()
【解析】
(1)利用等边三角形的性质可得AB=AC,又因为AD=AC已知,所以AB=AD,进而得到本题答案;
(2) 设∠3=∠D=x°,∠1=∠2=y°,利用等边三角形的性质以及三角形内角和定理得出∠3+∠D+∠BAD=180°,进而得出答案;
(3)首先得出△ABE≌△ADG ,进而得出∠4=∠AEB=60°,进而求出DE=BG=2GF, AG= BG=2GF, AF=AG+GF=3FG,即可得出答案.
解:(1)∵AB=AC,AD=AC,
∴AB=AD,
∴∠3=∠D(即∠ABD=∠D)
(2)∵AE平分∠CAD,
∴∠1=∠2,
∵△ABC是等边三角形,
∴∠BAC=60°,
设∠3=∠D=x°,∠1=∠2=y°,
∵∠3+∠D+∠BAD=180°,
∴x +x + 60° +2y =180°,
∴x +y =60°,
∴∠AEB=∠1+∠D = x +y = 60°;
(3)∵BG=DE,
∴BE=DG,
在△ABE和△ADG中,
![]()
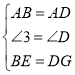 ,
,
∴△ABE≌△ADG(SAS)
∴∠4=∠AEB=60°
∵△ABC是等边三角形,F是BC中点,
∴∠AFB=90°,∠7=30°,
∵∠6=90°﹣∠5=30°,
∴DE=BG=2GF,
∵∠3=60°﹣∠6=30°=∠7,
∴AG=BG=2GF,
∴AF=AG+GF=3FG,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,点A,B,C均在格点上.
(1)请值接写出点A,B,C的坐标.
(2)若平移线段AB,使B移动到C的位置,请在图中画出A移动后的位置D,依次连接B,C,D,A,并求出四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“数学运算”是数学学科核心素养之一,某校对七年级学生“数学运算能力”情况进行调研,从该校360名七年级学生中抽取了部分学生进行运算能力测试井进行分析,成绩分为A、B、C三个层次,绘制了频数分布表(如下),请根据图表信息解答下列问题:

(1)补全频数分布;
(2)如果成绩为A等级的同学属于优秀,请你估计该校七年级约有多少人达到优秀水平?
-
科目: 来源: 题型:
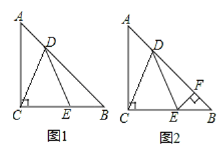
查看答案和解析>>【题目】△ABC中,AC=BC,∠ACB=90°,点D在AB上,E在BC上,且AD=BE,BD=AC.
(1)如图1,求证:DC=DE;
(2)如图2,过E作EF⊥AB于F,若BF=2,求CE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形
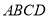 中,对角线
中,对角线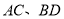 相交于点
相交于点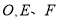 是对角线
是对角线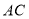 上的两点,给出下列四个条件:①
上的两点,给出下列四个条件:①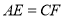 ;②
;②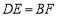 ;③
;③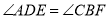 ;④
;④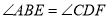 .其中能判定四边形
.其中能判定四边形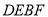 是平行四边形的有( )
是平行四边形的有( )
A.①B.①④C.①③④D.①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业前年按可回收垃圾处理费15元/吨、不可回收垃圾处理费25元/吨的收费标准,共支付两种垃圾处理费5000元,从去年元月起,收费标准上调为:可回收垃圾处理费30元/吨,不可回收垃圾处理费100元/吨.若该企业去年处理的这两种垃圾数量与前年相比没有变化,但调价后就要多支付处理费9000元.
(1)该企业前年处理的可回收垃圾和不可回收垃圾各多少吨?
(2)该企业计划今年将上述两种垃圾处理总量减少到200吨,且可回收垃圾不少于不可回收垃圾处理量的3倍,则今年该企业至少有多少吨可回收垃圾?
-
科目: 来源: 题型:
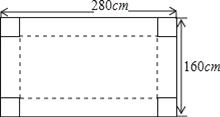
查看答案和解析>>【题目】我国水资源比较缺乏,人均水量约为世界人均水量的四分之一,其中西北地区缺水尤为严重.一村民为了蓄水,他把一块矩形白铁皮四个角各切去一个同样大小的小正方形后制作一个无盖水箱用于接雨水.已知白铁皮的长为280cm,宽为160cm(如图).
(1)若水箱的底面积为16000cm2,请求出切去的小正方形边长;
(2)对(1)中的水箱,若盛满水,这时水量是多少升?(注:1升水=1000cm3水)
相关试题

