【题目】如图,阳光下,小亮的身高如图中线段AB所示,他在地面上的影子如图中线段BC所示,线段DE表示旗杆的高,线段FG表示一堵高墙. 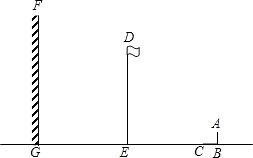
(1)请你在图中画出旗杆在同一时刻阳光照射下形成的影子;
(2)如果小亮的身高AB=1.6m,他的影子BC=2.4m,旗杆的高DE=15m,旗杆与高墙的距离EG=16m,请求出旗杆的影子落在墙上的长度.
参考答案:
【答案】
(1)解:如图:线段MG和GE就表示旗杆在阳光下形成的影子

(2)解:过M作MN⊥DE于N,
设旗杆的影子落在墙上的长度为x,由题意得:△DMN∽△ACB,
∴ ![]()
又∵AB=1.6,BC=2.4,
DN=DE﹣NE=15﹣x
MN=EG=16
∴ ![]()
解得:x= ![]() ,
,
答:旗杆的影子落在墙上的长度为 ![]() 米
米
【解析】(1)连接AC,过D点作AC的平行线即可;(2)过M作MN⊥DE于N,利用相似三角形列出比例式求出旗杆的高度即可.
【考点精析】利用相似三角形的应用和平行投影对题目进行判断即可得到答案,需要熟知测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解;太阳光线可以看成是平行光线,平行光线所形成的投影称为平行投影;作物体的平行投影:由于平行投影的光线是平行的,而物体的顶端与影子的顶端确定的直线就是光线,故根据另一物体的顶端可作出其影子.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为4,点E、F分别在边AB,BC上,且AE=BF=1,则OC=

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋里装有分别标有汉字“美”、“丽”、“南”、“山”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,求摸出球上的汉字刚好是“美”的概率;
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图或列表法,求甲取出的两个球上的汉字恰能组成“美丽”或“南山”的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某班组织去方特参加秋季社会实践活动,其中第一小组有x人,第二小组的人数比第一小组人数的
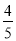 少30人,如果从第二小组调出10人到第一小组,那么:
少30人,如果从第二小组调出10人到第一小组,那么:(1)两个小组共有多少人?
(2)调动后,第一小组的人数比第二小组多多少人?
-
科目: 来源: 题型:
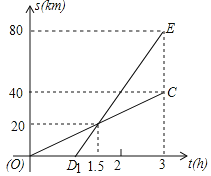
查看答案和解析>>【题目】已知A、B两地相距80km,甲、乙两人沿同一条公路从A地到B地,乙骑自行车,甲骑摩托车,DE、OC分别表示甲、乙两人离开A地的距离(km)与乙出发的时间(h)的关系,根据图象填空:
(1)乙先出发__h后,甲才出发;
(2)大约在乙出发后__h,两人相遇,这时他们离A地__km;
(3)甲到达B地时,乙离开A地__km;
(4)甲的速度是__km/h;乙的速度是__km/h;
(5)甲离开A地的距离s(km)与乙出发的时间t(h)的关系式为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在解决问题:已知a=
 ,求2a2﹣8a+1的值,他是这样分析与解的:
,求2a2﹣8a+1的值,他是这样分析与解的:∵a=
 =
= =2﹣
=2﹣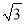
∴a﹣2=﹣

∴(a﹣2)2=3,a2﹣4a+4=3
∴a2﹣4a=﹣1
∴2a2﹣8a+1=2(a2﹣4a)+1=2×(﹣1)+1=﹣1
请你根据小明的分析过程,解决如下问题:
(1)化简
 +
+ +
+ +…+
+…+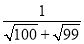
(2)若a=
 ,求4a2﹣8a+1的值.
,求4a2﹣8a+1的值. -
科目: 来源: 题型:
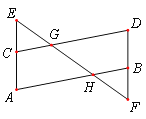
查看答案和解析>>【题目】已知:如图,∠A=∠D,∠EGC=∠FHB
(1)求证:AB∥CD
(2)求证:∠E=∠F
相关试题

