【题目】已知:平面直角坐标系中,A(a,3)、B(b,6)、C(c,1),a、b、c都为实数,并且满足3b-5c=-2a-18,4b-c=3a+10
(1) 请直接用含a的代数式表示b和c
(2) 当实数a变化时,判断△ABC的面积是否发生变化?若不变,求其值;若变化,求其变化范围
(3) 当实数a变化时,若线段AB与y轴相交,线段OB与线段AC交于点P,且S△PAB>S△PBC,求实数a的取值范围.


参考答案:
【答案】(1)![]() ;(2)S△ABC=13为定值;(3)
;(2)S△ABC=13为定值;(3)![]()
【解析】
(1)由4b-c=3a+10可知c=4b-3a-10,把c代入3b-5c=-2a-18可用a 表示出b,同理可表示c;(2)如图构造梯形,根据S△ABC=S梯形ADEC-S△ADB-S△CBE可证明S△ABC是定值,所以△ABC的面积无变化;(3)作AD⊥x轴,BE⊥x轴,CF⊥x轴,根据S△PAB>S△PBC可知AP>PC,进而可得S△OAP>S△OPC,所以S△OAB>S△OBC,利用梯形和三角形的面积差可表示出△OAB和△OBC的面积,即可列出不等式,由AB与y轴相交可得-4≤a≤0,结合前面的不等式求出公共解集即可求出a的取值范围.
(1)∵4b-c=3a+10,
∴c=4b-3a-10,
∵3b-5c=-2a-18,
∴3b-5(4b-3a-10)=-2a-18,
∴b=a+4,
同理可得:c=a+6,
∴![]()
(2) 构造如图所示的梯形:
S△ABC=![]()
![]() (3+5)
(3+5)![]() 6-
6-![]()
![]() 3
3![]() 4-
4-![]()
![]() 2
2![]() 5=13为定值,
5=13为定值,

(3) 线段AB与y轴相交,故![]() ,
,
∴-4≤a≤0,
∵S△PAB>S△PBC,
∴AP>PC,
∴S△OAP>S△OPC,
∴S△OAB>S△OBC,
作AD⊥x轴,BE⊥x轴,CF⊥x轴,

S△OAB=![]() (3+6)
(3+6)![]() -
-![]()
![]()
![]() 6-
6-![]()
![]() 6
6![]() =6-
=6-![]() a,
a,
S△OBC=![]()
![]() (1+6)(
(1+6)(![]() )+
)+![]()
![]()
![]() 6-
6-![]()
![]() =
=![]() a+16,
a+16,
∴6-![]() a>
a>![]() a+16,
a+16,
解得:a<-![]() ,
,
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是菱形,点E、F分别是菱形ABCD边AD、CD的中点.
(1)求证:BE=BF;
(2)当△BEF为等边三角形时,求
 的度数.
的度数.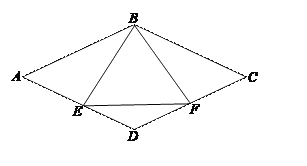
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
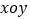 中,直线
中,直线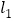 经过点
经过点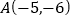 且与直线
且与直线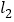 :
: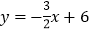 平行,直线
平行,直线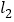 与
与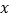 轴、
轴、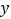 轴分别交于点B、C.
轴分别交于点B、C.(1)求直线l1的表达式及其与
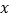 轴的交点D的坐标;
轴的交点D的坐标;(2)判断四边形ABCD是什么四边形?并证明你的结论;
(3)若点E是直线AB上一点,平面内存在一点F,使得四边形CBEF是正方形,求点E的坐标,请直接写出答案.

-
科目: 来源: 题型:
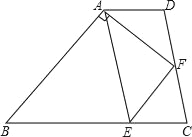
查看答案和解析>>【题目】如图,梯形ABCD中,AD∥BC,点E在BC上,AE=BE,点F是CD的中点,且AF⊥AB,若AD=2.7,AF=4,AB=6,则CE的长为( )
A. 2
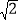 B. 2
B. 2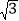 -1 C. 2.5 D. 2.3
-1 C. 2.5 D. 2.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D,E分别在AC、BC边上运动,且保持AD=CE,连接DE,DF,EF,在此运动过程中,下列结论:(1)△DFE是等腰直角三角形;(2)DE长度的最小值为4;(3)四边形CDFE的面积保持不变;(4)△CDE面积的最大值是4.正确的结论是( )

A. (1)(2)(3) B. (1)(3)(4) C. (1)(2)(4) D. (2)(3)(4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AC=3,BC=4.分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BDMC,四块阴影部分的面积分别为S1、S2、S3、S4.则S1+S2+S3+S4等于( )
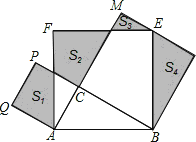
A.14 B.16 C.18 D.20
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,E,F是对角线AC上的两点且AE=CF,在①BE=DF;②BE∥DF;③AB=DE;④四边形EBFD为平行四边形;⑤S△ADE=S△ABE;⑥AF=CE这些结论中正确的是_____.
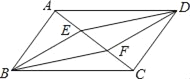
相关试题

