【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 经过点
经过点![]() 且与直线
且与直线![]() :
:![]() 平行,直线
平行,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点B、C.
轴分别交于点B、C.
(1)求直线l1的表达式及其与![]() 轴的交点D的坐标;
轴的交点D的坐标;
(2)判断四边形ABCD是什么四边形?并证明你的结论;
(3)若点E是直线AB上一点,平面内存在一点F,使得四边形CBEF是正方形,求点E的坐标,请直接写出答案.

参考答案:
【答案】(1)![]() (-9,0);(2)四边形ABCD是矩形;(3)(-2,-4),(10,4)
(-9,0);(2)四边形ABCD是矩形;(3)(-2,-4),(10,4)
【解析】(1)根据,直线![]() 与直线
与直线![]() 平行,设出
平行,设出![]() 的函数关系式,再利用待定系数法即可求出
的函数关系式,再利用待定系数法即可求出![]() 的函数关系式,再令
的函数关系式,再令![]() ,即可求出点D坐标;
,即可求出点D坐标;
(2)利用平面内两点间的距离公式求出AD与BC的长相等,再根据AD∥BC及BD=AC,即可求出结论;
(3)根据正方形的判定,作出图形,即可得出点E的坐标.
详解:(1)∵直线![]() 与直线
与直线![]() :
:![]() 平行,
平行,
∴设![]() ,
,
∵直线![]() 经过点
经过点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
当![]() 时,
时,
![]() ,
,
解得![]() ,
,
∴![]() .
.
(2)四边形ABCD是矩形.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵AD∥BC,
∴四边形ABCD是平行四边形,
∵![]() ,
,![]() ,
,
∴BD=AC,
∴平行四边形ABCD是矩形.
(3)如图所示,
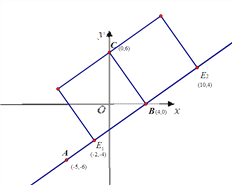
点E坐标为:![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AEF=80°,且∠A=x°,∠C=y°,∠F=z°.若
 +|y-80-m|+|z-40|=0(m为常数,且0<m<100)
+|y-80-m|+|z-40|=0(m为常数,且0<m<100)(1) 求∠A、∠C的度数(用含m的代数式表示)
(2) 求证:AB∥CD
(3) 若∠A=40°,∠BAM=20°,∠EFM=10°,直线AM与直线FM交于点M,直接写出∠AMF的度数


-
科目: 来源: 题型:
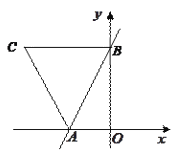
查看答案和解析>>【题目】如图,已知一次函数
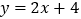 的图像与x轴、
的图像与x轴、 轴分别交于点A、B,且BC∥AO,梯形AOBC的面积为10.
轴分别交于点A、B,且BC∥AO,梯形AOBC的面积为10.(1)求点A、B、C的坐标;
(2)求直线AC的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是菱形,点E、F分别是菱形ABCD边AD、CD的中点.
(1)求证:BE=BF;
(2)当△BEF为等边三角形时,求
 的度数.
的度数.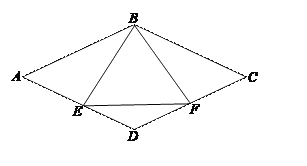
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,梯形ABCD中,AD∥BC,点E在BC上,AE=BE,点F是CD的中点,且AF⊥AB,若AD=2.7,AF=4,AB=6,则CE的长为( )
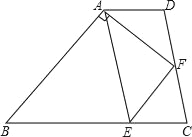
A. 2
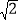 B. 2
B. 2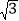 -1 C. 2.5 D. 2.3
-1 C. 2.5 D. 2.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:平面直角坐标系中,A(a,3)、B(b,6)、C(c,1),a、b、c都为实数,并且满足3b-5c=-2a-18,4b-c=3a+10
(1) 请直接用含a的代数式表示b和c
(2) 当实数a变化时,判断△ABC的面积是否发生变化?若不变,求其值;若变化,求其变化范围
(3) 当实数a变化时,若线段AB与y轴相交,线段OB与线段AC交于点P,且S△PAB>S△PBC,求实数a的取值范围.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D,E分别在AC、BC边上运动,且保持AD=CE,连接DE,DF,EF,在此运动过程中,下列结论:(1)△DFE是等腰直角三角形;(2)DE长度的最小值为4;(3)四边形CDFE的面积保持不变;(4)△CDE面积的最大值是4.正确的结论是( )

A. (1)(2)(3) B. (1)(3)(4) C. (1)(2)(4) D. (2)(3)(4)
相关试题

