【题目】如图,已知∠MON=30°,点A1、A2、A3……在射线ON上,点B1、B2、B3……在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4……均为等边三角形,且OA1=1.
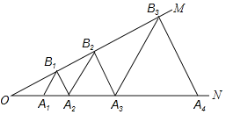
(1)分别求出△A1B1A2、△A3B3A4的边长;
(2)求△A7B7A8的周长(直接写出结果).
参考答案:
【答案】(1)1,4;(2)198.
【解析】
(1)根据等腰三角形的性质以及平行线的性质得出A1B1∥A2B2∥A3B3,以及A2B2=2B1A2,得出A3B3=4B1A2=4,可得结论;
(2)由(1)同理得:A4B4=8B1A2=8,A5B5=16B1A2…进而得出答案.
解:(1)如图,
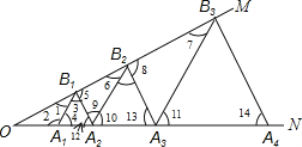
∵△A1B1A2是等边三角形,
∴A1B1=A2B1,∠3=∠4=∠12=60°,
∴∠2=120°,
∵∠MON=30°,
∴∠1=180°-120°-30°=30°,
∴∠1=∠MON=30°,
∴A1B1=OA1=1,即△A1B1A2的边长为1;
又∵∠3=60°,
∴∠5=180°-60°-30°=90°,
∵A2B1=1,
∴A2B2=2A2B1=2,即△A2B2A3的边长为2;
∵△A2B2A3、△A3B3A4是等边三角形,
∴∠11=∠10=60°,∠13=60°,
∵∠4=∠12=60°,
∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,
∴∠1=∠6=∠7=30°,∠5=∠8=90°,
∴A2B2=2B1A2,B3A3=2B2A3,
∴A3B3=4B1A2=4,即△A3B3A4的边长为4;
综上,△A1B1A2的边长为1;△A3B3A4的边长为4;
(2)△A7B7A8的周长是198.
解:由(1)同理得:A4B4=8B1A2=8=23,
A5B5=16B1A2=16=24,
以此类推:A7B7=26=64;
∴△A7B7A8的周长=3×64=198.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一个图形,通过两种不同的方法计算它们的面积,可以得到一个数学等式,例如图1可以得到
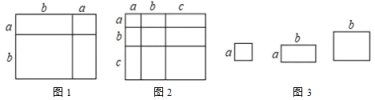
(1)类似图1的数学等式,写出图2表示的数学等式;
(2)若
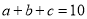 ,
, 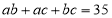 ,用上面得到的数学等式乘
,用上面得到的数学等式乘 的值;
的值;(3)小明同学用图3中的
 张边长为
张边长为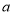 的正方形,
的正方形,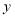 张边长为
张边长为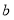 的正方形,z张边长为
的正方形,z张边长为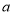 、
、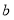 的长方形拼出一个面积为
的长方形拼出一个面积为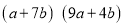 的长方形,求
的长方形,求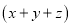 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的对称中心在坐标原点,AB∥x轴,AD、BC分别与x轴交于E、F,连接BE、DF,若正方形ABCD有两个顶点在双曲线y=
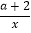 上,实数a满足a3﹣a=1,则四边形DEBF的面积是_____.
上,实数a满足a3﹣a=1,则四边形DEBF的面积是_____.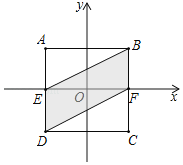
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
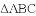 中,
中, ,作AB边的垂直平分线交直线BC于M,交AB于点N.
,作AB边的垂直平分线交直线BC于M,交AB于点N.
(1)如图
 ,若
,若 ,则
,则 =_________度;
=_________度;(2)如图
 ,若
,若 ,则
,则 =_________度;
=_________度;(3)如图
 ,若
,若 ,则
,则 =________度;
=________度;(4)由
 问,你能发现
问,你能发现 与∠A有什么关系?写出猜想,并证明。
与∠A有什么关系?写出猜想,并证明。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知两种不同的数对处理器
 、
、 .当数对
.当数对 输入处理器
输入处理器 时,输出数对
时,输出数对 ,记作
,记作 ,
, ,
, ;但数对
;但数对 输入处理器
输入处理器 时,输出数对
时,输出数对 ,记作
,记作 ,
, ,
, .
.(1)
 ,
, ( , ),
( , ), ,
, ( , ).
( , ).(2)当
 ,
, ,
, 时,求
时,求 ,
, ;
;(3)对于数对
 ,
, ,
, ,
, 一定成立吗?若成立,说明理由;若不成立,举例说明.
一定成立吗?若成立,说明理由;若不成立,举例说明. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在△ABC中,∠A<90°,P是BC边上的一点,P1,P2是点P关于AB、AC的对称点,连结P1P2,分别交AB、AC于点D、E.
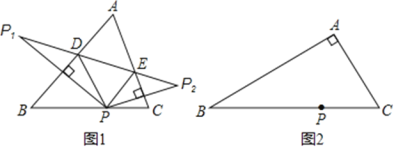
(1)若∠A=52°,求∠DPE的度数;
(2)如图2,在△ABC中,若∠BAC=90°,用三角板作出点P关于AB、AC的对称点P1、P2,(不写作法,保留作图痕迹),试判断点P1,P2与点A是否在同一直线上,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线AM⊥AN,AB平分∠MAN,过点B作BC⊥BA交AN于点C;动点E、D同时从A点出发,其中动点E以2cm/s的速度沿射线AN方向运动,动点D以1cm/s的速度运动;已知AC=6cm,设动点D,E的运动时间为t.
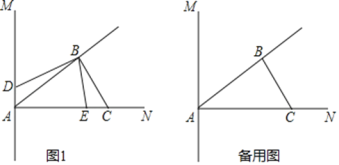
(1)当点D在射线AM上运动时满足S△ADB:S△BEC=2:1,试求点D,E的运动时间t的值;
(2)当动点D在直线AM上运动,E在射线AN运动过程中,是否存在某个时间t,使得△ADB与△BEC全等?若存在,请求出时间t的值;若不存在,请说出理由.
相关试题

