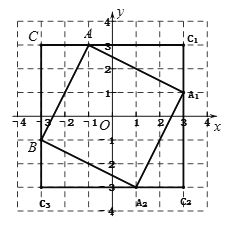
【题目】如图,在平面直角坐标系中,有一![]() ,且
,且![]() ,
,![]() ,
,![]() ,已知
,已知![]() 是由
是由![]() 绕某点顺时针旋转得到的.
绕某点顺时针旋转得到的.

(1)请写出旋转中心的坐标是 ,旋转角是 度;
(2)以(1)中的旋转中心为中心,分别画出![]() 顺时针旋转90°、180°的三角形;
顺时针旋转90°、180°的三角形;
(3)设![]() 两直角边
两直角边![]() 、
、![]() 、斜边
、斜边![]() ,利用变换前后所形成的图案验证勾股定理.
,利用变换前后所形成的图案验证勾股定理.
参考答案:
【答案】(1)旋转中心坐标是![]() ,旋转角是
,旋转角是![]() ;(2)见解析;(3)见解析
;(2)见解析;(3)见解析
【解析】
(1)由图形可知,对应点的连线CC1、AA1的垂直平分线过点O,根据旋转变换的性质,点O即为旋转中心,再根据网格结构,观察可得旋转角为90°;
(2)利用网格结构,分别找出旋转后对应点的位置,然后顺次连接即可;
(3)利用面积,根据正方形CC1C2C3的面积等于正方形AA1A2B的面积加上△ABC的面积的4倍,列式计算即可得证.
(1)旋转中心坐标是![]() ,旋转角是
,旋转角是![]()
(2)画出图形如图所示.
(3)由旋转的过程可知,四边形![]() 和四边形
和四边形![]() 是正方形.
是正方形.
∵![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() .
.
即![]() 中,
中,![]() ,
,![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线L与y=2x+1的交于点A(2,a),与直线y=x+2的交于点B(b,1)
(1)求a,b的值;
(2)求直线l的函数表达式;
(3)求直线L、x轴、直线y=2x+1围成的图形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的说理过程:如图,在四边形
 中,
中, ,
, 分别是
分别是 ,
, 延长线上的点,连接
延长线上的点,连接 ,分别交
,分别交 ,
, 于点
于点 ,
, .已知
.已知 ,
, .对
.对 和
和 说明理由.
说明理由.
理由:
 (已知),
(已知), (______),
(______), (等量代换).
(等量代换).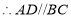 (______).
(______). (______).
(______). (______),
(______), (______).
(______). (______).
(______). -
科目: 来源: 题型:
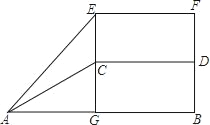
查看答案和解析>>【题目】如图是某个大型商场的自动扶梯侧面示意图,已知自动扶梯AC的坡度为1:2,AC的长度为5
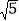 米,AB为底楼地面,CD为二楼侧面,EF为二楼楼顶,当然有EF∥AB∥CD,E为自动扶梯AC的最高端C的正上方,过C的直线EG⊥AB于G,在自动扶梯的底端A测得E的仰角为42°,求该商场二楼的楼高CE.
米,AB为底楼地面,CD为二楼侧面,EF为二楼楼顶,当然有EF∥AB∥CD,E为自动扶梯AC的最高端C的正上方,过C的直线EG⊥AB于G,在自动扶梯的底端A测得E的仰角为42°,求该商场二楼的楼高CE.(参考数据:sin42°=
 ,cos42°=
,cos42°= ,tan42°=
,tan42°=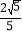 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是边长为6的等边△ABC三边中垂线的交点,将△ABC绕点O逆时针方向旋转180°,得到△A1B1C1,则图中阴影部分的面积为_____.
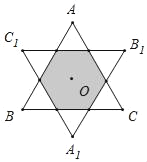
-
科目: 来源: 题型:
查看答案和解析>>【题目】自2019年5月30日万州牌楼长江大桥正式通车以来,大放光彩,引万人驻足.市民们纷纷前往打卡、拍照留念,因此牌楼长江大桥成为了万州网红打卡地.周末,小棋和小艺两位同学相约前往参观,小棋骑自行车,小艺步行,她们同时从学校出发,沿同一条路线前往,出发一段时间后小棋发现东西忘了,于是立即以原速返回到学校取,取到东西后又立即以原速追赶小艺并继续前往,到达目的地后等待小艺一起参观(取东西的时间忽略不计),在整个过程两人保持匀速,如图是两人之间的距离
 与出发时间
与出发时间 之间的函数图象如图所示,则当小棋到达目的地时,小艺离目的地还有______米.
之间的函数图象如图所示,则当小棋到达目的地时,小艺离目的地还有______米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△
 内接于⊙
内接于⊙ ,
,  60°,
60°, 是⊙
是⊙ 的直径,点
的直径,点 是
是 延长线上的一点,且
延长线上的一点,且 .
.(1)求证:
 是⊙
是⊙ 的切线;
的切线;(2)若
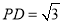 ,求⊙
,求⊙ 的直径.
的直径.
相关试题

