【题目】如图,△![]() 内接于⊙
内接于⊙![]() ,
, ![]() 60°,
60°,![]() 是⊙
是⊙![]() 的直径,点
的直径,点![]() 是
是![]() 延长线上的一点,且
延长线上的一点,且![]() .
.
(1)求证: ![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)若![]() ,求⊙
,求⊙![]() 的直径.
的直径.

参考答案:
【答案】(1)证明见解析;(2)⊙![]() 的直径为
的直径为![]()
【解析】试题分析:(1)连结AD,OA,如图,根据圆周角定理得∠DAC=90°,∠ADC=∠B=60°,则利用三角形内角和定理得∠ACD=30°,由于AP=AC,利用等腰三角形的性质易得∠P=30°.可得△OAD为等边三角形,则∠DOA=60°,而∠P=30°,则可计算出∠OAP=90°,然后根据切线的判定定理得到PA是⊙O的切线;
(2)在Rt△APO中,根据含30度的直角三角形性质得到OA=![]() OP,即OD+PD=2OA,而OD=OA,于是有OA=PD=
OP,即OD+PD=2OA,而OD=OA,于是有OA=PD=![]() ,从而得到圆的直径.
,从而得到圆的直径.
【解答】(1)证明:连结AD,OA,如图,

∵CD是⊙O的直径,
∴∠DAC=90°,
∵∠ADC=∠B=60°,
∴∠ACD=30°,
∵AP=AC,
∴∠P=∠ACP=30°.
∵OD=OA,∠ADO=60°,
∴△OAD为等边三角形,
∴∠DOA=60°,
而∠P=30°,
∴∠OAP=90°,
∴OA⊥AP,
∴PA是⊙O的切线;
(2)解:在Rt△APO中,∵∠P=30°,
∴OA=![]() OP,即OD+PD=2OA,
OP,即OD+PD=2OA,
而OD=OA,
∴OA=PD=![]() ,
,
∴⊙O的直径为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,有一
 ,且
,且 ,
, ,
, ,已知
,已知 是由
是由 绕某点顺时针旋转得到的.
绕某点顺时针旋转得到的.
(1)请写出旋转中心的坐标是 ,旋转角是 度;
(2)以(1)中的旋转中心为中心,分别画出
 顺时针旋转90°、180°的三角形;
顺时针旋转90°、180°的三角形;(3)设
 两直角边
两直角边 、
、 、斜边
、斜边 ,利用变换前后所形成的图案验证勾股定理.
,利用变换前后所形成的图案验证勾股定理. -
科目: 来源: 题型:
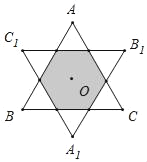
查看答案和解析>>【题目】如图,O是边长为6的等边△ABC三边中垂线的交点,将△ABC绕点O逆时针方向旋转180°,得到△A1B1C1,则图中阴影部分的面积为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】自2019年5月30日万州牌楼长江大桥正式通车以来,大放光彩,引万人驻足.市民们纷纷前往打卡、拍照留念,因此牌楼长江大桥成为了万州网红打卡地.周末,小棋和小艺两位同学相约前往参观,小棋骑自行车,小艺步行,她们同时从学校出发,沿同一条路线前往,出发一段时间后小棋发现东西忘了,于是立即以原速返回到学校取,取到东西后又立即以原速追赶小艺并继续前往,到达目的地后等待小艺一起参观(取东西的时间忽略不计),在整个过程两人保持匀速,如图是两人之间的距离
 与出发时间
与出发时间 之间的函数图象如图所示,则当小棋到达目的地时,小艺离目的地还有______米.
之间的函数图象如图所示,则当小棋到达目的地时,小艺离目的地还有______米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,能用
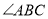 ,
,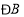 ,
,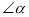 表示同一个角的是( )
表示同一个角的是( )A.
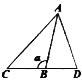 B.
B.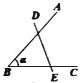 C.
C.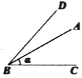 D.
D.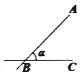
-
科目: 来源: 题型:
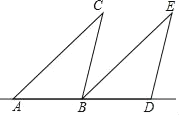
查看答案和解析>>【题目】如图,将△ABC沿直线AB向右平移后到达△BDE的位置.
(1)若AC=6cm,则BE= cm;
(2)若∠CAB=50°,∠BDE=100°,求∠CBE的度数.
-
科目: 来源: 题型:
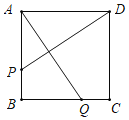
查看答案和解析>>【题目】如图,在正方形ABCD中,AB=8厘米,如果动点P在线段AB上以2厘米/秒的速度由A点向B点运动,同时动点Q在以1厘米/秒的速度线段BC上由C点向B点运动,当点P到达B点时整个运动过程停止.设运动时间为t秒,当AQ⊥DP时,t的值为_____秒.
相关试题

