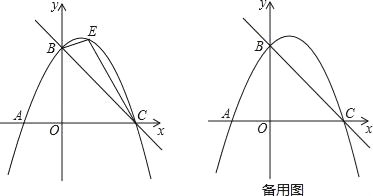
【题目】如图,直线y=﹣![]() x+4与x轴交于点C,与y轴交于点B,抛物线y=ax2+
x+4与x轴交于点C,与y轴交于点B,抛物线y=ax2+![]() x+c经过B、C两点.
x+c经过B、C两点.
(1)求抛物线的解析式;
(2)如图,点E是直线BC上方抛物线上的一动点,当△BEC面积最大时,请求出点E的坐标;
(3)在(2)的结论下,过点E作y轴的平行线交直线BC于点M,连接AM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
参考答案:
【答案】(1)y=﹣![]() x2+
x2+![]() x+4;(2)E(3,8);(3)点P的坐标是(﹣2,﹣
x+4;(2)E(3,8);(3)点P的坐标是(﹣2,﹣![]() )或(6,0)或(0,4).
)或(6,0)或(0,4).
【解析】试题分析:(1)首先根据直线![]() 与x轴交于点C,与y轴交于点B,求出点B的坐标是
与x轴交于点C,与y轴交于点B,求出点B的坐标是![]() ,点C的坐标是
,点C的坐标是![]() 然后根据抛物线
然后根据抛物线![]() 经过
经过![]() 两点,求出
两点,求出![]() 的值是多少,即可求出抛物线的解析式.
的值是多少,即可求出抛物线的解析式.
(2)首先过过E作EG∥y轴,交直线BC于G,然后设![]() 则
则![]() 求出
求出![]() 的值是多少;最后根据三角形的面积的求法,求出
的值是多少;最后根据三角形的面积的求法,求出![]() 进而判断出当
进而判断出当![]() 面积最大时,点E的坐标和
面积最大时,点E的坐标和![]() 面积的最大值各是多少即可.
面积的最大值各是多少即可.
(3)在抛物线上存在点P,使得以![]() 为顶点的四边形是平行四边形.然后分三种情况讨论,根据平行四边形的特征,求出使得以
为顶点的四边形是平行四边形.然后分三种情况讨论,根据平行四边形的特征,求出使得以![]() 为顶点的四边形是平行四边形的点P的坐标是多少即可.
为顶点的四边形是平行四边形的点P的坐标是多少即可.
试题解析:(1)当![]() 时,
时, ![]()
∴![]() ,
,
当![]() 时,
时, ![]()
![]() ∴
∴![]()
把![]() 和
和![]() 代入抛物线
代入抛物线![]() 中得:
中得:

解得:  ,
,
∴抛物线的解析式为: ![]()
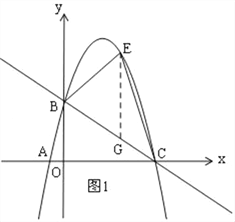
(2)如图1,过E作EG∥y轴,交直线BC于G,
设![]() 则
则![]()
![]()
![]()
∵![]()
∴S有最大值,此时![]()
(3)![]()
对称轴是: ![]()
∴![]()
在抛物线上存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形.
如图2,以AM为边时,由(2),可得点M的横坐标是3,
∵点M在直线![]() 上,
上,
∴点M的坐标是(3,2),
又∵点A的坐标是(﹣1,0),点Q的横坐标为2,
根据M到Q的平移规律:可知:P的横坐标为﹣2,
∴![]()
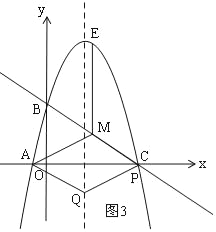
②如图3,以AM为边时,四边形AMPQ是平行四边形,
由(2),可得点M的横坐标是2,
∵A(﹣1,0),且Q的横坐标为2,
∴P的横坐标为6,
∴P(6,0)(此时P与C重合);
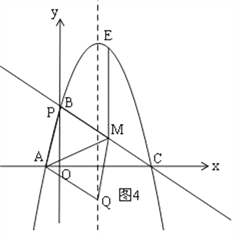
③以AM为对角线时,如图4,
∵M到Q的平移规律可得P到A的平移规律
∴点P的坐标是(0,4)
综上所述,在抛物线上存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形,
点P的坐标是![]() 或(6,0)或(0,4).
或(6,0)或(0,4).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若点A在数轴上对应的数为a,点B在数轴上对应的数为b,点C在数轴上对应的数为c,且|a+2|+(b﹣1)2=0,2c﹣1=
 c+2.
c+2.
(1)求线段AB的长;
(2)在数轴上是否存在点P,使得PA+PB=PC?若存在,求出点P对应的数;若不存在,说明理由.
(3)现在点A,B,C开始在数轴上运动,若点A以每秒1个单位长度向左运动,同时,点B和点C分别以每秒4个单位长度和9个单位长度的速度向右运动.假设t秒后,点B和点C之间的距离表示为BC,点A和点B之间的距离表示为AB.请问AB﹣BC的值是否随着时间t的变化而变化?若变化,请说明理由;若不变,请求出常数值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在研究反比例函数y=﹣
 的图象时,我们发现有如下性质:
的图象时,我们发现有如下性质:(1)y=﹣
 的图象是中心对称图形,对称中心是原点.
的图象是中心对称图形,对称中心是原点.(2)y=﹣
 的图象是轴对称图形,对称轴是直线y=x,y=﹣x.
的图象是轴对称图形,对称轴是直线y=x,y=﹣x.(3)在x<0与x>0两个范围内,y随x增大而增大;
类似地,我们研究形如:y=﹣
 +3的函数:
+3的函数:(1)函数y=﹣
 +3图象是由反比例函数y=﹣
+3图象是由反比例函数y=﹣ 图象向____平移______个单位,再向_______平移______个单位得到的.
图象向____平移______个单位,再向_______平移______个单位得到的.(2)y=﹣
 +3的图象是中心对称图形,对称中心是______.
+3的图象是中心对称图形,对称中心是______.(3)该函数图象是轴对称图形吗?如果是,请求出它的对称轴,如果不是,请说明理由.
(4)对于函数y=
 ,x在哪些范围内,y随x的增大而增大?
,x在哪些范围内,y随x的增大而增大? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一个三角形纸片ACB,其中∠ACB=90°,AC=8,BC=6,E、F分别是AC、AB边上的点,连接EF.(1)如图1,若将纸片ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,且使S四边形ECBF=4S△EDF,求ED的长;
(2)如图2,若将纸片ACB的一角沿EF折叠,折叠后点A落在BC边上的点M处,且使MF∥CA.
①试判断四边形AEMF的形状,并证明你的结论;
②求EF的长;
(3)如图3,若FE的延长线与BC的延长线交于点N,CN=2,CE=
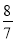 ,求
,求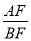 的值.
的值.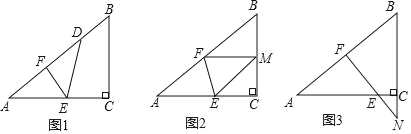
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于反比例函数
 ,下列说法中不正确的是( )
,下列说法中不正确的是( )A. 图像经过点(1.-2)
B. 图像分布在第二第四象限
C. x>0时,y随x增大而增大
D. 若点A(
 )B(
)B( )在图像上,若
)在图像上,若 ,则
,则
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图两张长相等,宽分别是1和3的矩形纸片上叠合在一起,重叠部分为四边形ABCD,且AB+BC=6,则四面行ABCD的面积为( )

A. 3B.
 C. 9D.
C. 9D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
 的图像经过点A(-1,0),并与反比例函数
的图像经过点A(-1,0),并与反比例函数 (
( )的图像交于B(m,4)
)的图像交于B(m,4)
(1)求
 的值;
的值;(2)以AB为一边,在AB的左侧作正方形
 ,求C点坐标;
,求C点坐标;(3)将正方形
 沿着
沿着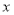 轴的正方向,向右平移n个单位长度,得到正方形
轴的正方向,向右平移n个单位长度,得到正方形 ,线段
,线段 的中点为点
的中点为点 ,若点
,若点 和点
和点 同时落在反比例函数
同时落在反比例函数 的图像上,求n的值.
的图像上,求n的值.
相关试题

