【题目】在研究反比例函数y=﹣![]() 的图象时,我们发现有如下性质:
的图象时,我们发现有如下性质:
(1)y=﹣![]() 的图象是中心对称图形,对称中心是原点.
的图象是中心对称图形,对称中心是原点.
(2)y=﹣![]() 的图象是轴对称图形,对称轴是直线y=x,y=﹣x.
的图象是轴对称图形,对称轴是直线y=x,y=﹣x.
(3)在x<0与x>0两个范围内,y随x增大而增大;
类似地,我们研究形如:y=﹣![]() +3的函数:
+3的函数:
(1)函数y=﹣![]() +3图象是由反比例函数y=﹣
+3图象是由反比例函数y=﹣![]() 图象向____平移______个单位,再向_______平移______个单位得到的.
图象向____平移______个单位,再向_______平移______个单位得到的.
(2)y=﹣![]() +3的图象是中心对称图形,对称中心是______.
+3的图象是中心对称图形,对称中心是______.
(3)该函数图象是轴对称图形吗?如果是,请求出它的对称轴,如果不是,请说明理由.
(4)对于函数y=![]() ,x在哪些范围内,y随x的增大而增大?
,x在哪些范围内,y随x的增大而增大?
参考答案:
【答案】(1)右,2,上,3;(2)(2,3);(3)是轴对称图形,对称轴是:y=x+1和y=﹣x+5;(4)x<2或x>2.
【解析】
(1)根据图象平移的法则即可解答;
(2)根据平移的方法,函数y=﹣![]() 的中心原点平移后的点就是对称中心;
的中心原点平移后的点就是对称中心;
(3)图象平移后与原来的直线y=x和y=-x平行,并且经过对称中心,利用待定系数法即可求解;
(4)把已知的函数y=![]() 变形成的形式
变形成的形式![]() ,类比反比例函数性质即可解答.
,类比反比例函数性质即可解答.
解:(1)函数y=﹣![]() +3图象是由反比例函数y=﹣
+3图象是由反比例函数y=﹣![]() 图象向右平移 2个单位,再向上平移3个单位得到的.
图象向右平移 2个单位,再向上平移3个单位得到的.
故答案为:右2上3.
(2)y=﹣![]() +3的图象是中心对称图形,对称中心是(2,3).
+3的图象是中心对称图形,对称中心是(2,3).
故答案为:(2,3).
(3)该函数图象是轴对称图形.
∵y=﹣![]() 的图象是轴对称图形,对称轴是直线y=x,y=﹣x.
的图象是轴对称图形,对称轴是直线y=x,y=﹣x.
设y=﹣![]() +3对称轴是y=x+b,把(2,3)代入得:3=2+b,
+3对称轴是y=x+b,把(2,3)代入得:3=2+b,
∴b=1,
∴对称轴是y=x+1;
设y=﹣![]() +3对称轴是y=﹣x+c,把(2,3)代入得:3=﹣2+c,
+3对称轴是y=﹣x+c,把(2,3)代入得:3=﹣2+c,
∴c=5.
∴对称轴是y=﹣x+5.
故答案为:y=x+1和y=﹣x+5.
(4)对于函数y=![]() ,变形得:
,变形得:
y=![]() =
=![]() =
=![]() ,
,
则其对称中心是(2,![]() ).
).
则当x<2或x>2时y随x的增大而增大.
故答案为:x<2或x>2
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司计划从两家皮具生产能力相近的制造厂选择一家来承担外销业务,这两家厂生产的皮具款式和材料都符合要求,因此只需要检测皮具质量的克数是否稳定,现从两家提供的样品中各抽取了6件进行检查,超过标准质量部分记为正数,不足部分记为负数,若该皮具的标准质量为500克,测得它们质量如下(单位:g)
厂家
超过标准质量的部分
甲
﹣3
0
0
1
2
0
乙
﹣2
1
﹣1
0
1
1
(1)分别计算甲、乙两厂抽样检测的皮具总质量各是多少克?
(2)通过计算,你认为哪一家生产皮具的质量比较稳定?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克)
50
60
70
销售量y(千克)
100
80
60
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),则当售价x定为多少元时,厂商每天能获得最大利润?最大利润是多少?
(3)如果超市要获得每天不低于1350元的利润,且符合超市自己的规定,那么该商品每千克售价的取值范围是多少?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若点A在数轴上对应的数为a,点B在数轴上对应的数为b,点C在数轴上对应的数为c,且|a+2|+(b﹣1)2=0,2c﹣1=
 c+2.
c+2.
(1)求线段AB的长;
(2)在数轴上是否存在点P,使得PA+PB=PC?若存在,求出点P对应的数;若不存在,说明理由.
(3)现在点A,B,C开始在数轴上运动,若点A以每秒1个单位长度向左运动,同时,点B和点C分别以每秒4个单位长度和9个单位长度的速度向右运动.假设t秒后,点B和点C之间的距离表示为BC,点A和点B之间的距离表示为AB.请问AB﹣BC的值是否随着时间t的变化而变化?若变化,请说明理由;若不变,请求出常数值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一个三角形纸片ACB,其中∠ACB=90°,AC=8,BC=6,E、F分别是AC、AB边上的点,连接EF.(1)如图1,若将纸片ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,且使S四边形ECBF=4S△EDF,求ED的长;
(2)如图2,若将纸片ACB的一角沿EF折叠,折叠后点A落在BC边上的点M处,且使MF∥CA.
①试判断四边形AEMF的形状,并证明你的结论;
②求EF的长;
(3)如图3,若FE的延长线与BC的延长线交于点N,CN=2,CE=
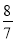 ,求
,求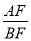 的值.
的值.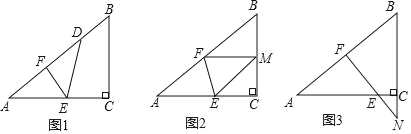
-
科目: 来源: 题型:
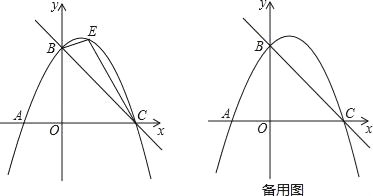
查看答案和解析>>【题目】如图,直线y=﹣
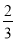 x+4与x轴交于点C,与y轴交于点B,抛物线y=ax2+
x+4与x轴交于点C,与y轴交于点B,抛物线y=ax2+ x+c经过B、C两点.
x+c经过B、C两点.(1)求抛物线的解析式;
(2)如图,点E是直线BC上方抛物线上的一动点,当△BEC面积最大时,请求出点E的坐标;
(3)在(2)的结论下,过点E作y轴的平行线交直线BC于点M,连接AM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于反比例函数
 ,下列说法中不正确的是( )
,下列说法中不正确的是( )A. 图像经过点(1.-2)
B. 图像分布在第二第四象限
C. x>0时,y随x增大而增大
D. 若点A(
 )B(
)B( )在图像上,若
)在图像上,若 ,则
,则
相关试题

