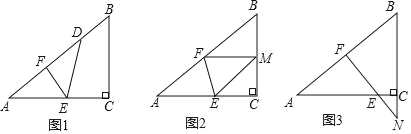
【题目】如图,已知一个三角形纸片ACB,其中∠ACB=90°,AC=8,BC=6,E、F分别是AC、AB边上的点,连接EF.(1)如图1,若将纸片ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,且使S四边形ECBF=4S△EDF,求ED的长;
(2)如图2,若将纸片ACB的一角沿EF折叠,折叠后点A落在BC边上的点M处,且使MF∥CA.
①试判断四边形AEMF的形状,并证明你的结论;
②求EF的长;
(3)如图3,若FE的延长线与BC的延长线交于点N,CN=2,CE=![]() ,求
,求![]() 的值.
的值.
参考答案:
【答案】(1)2![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)先利用折叠的性质得到![]() ,
, ![]() ≌
≌![]() ,则
,则![]() 则易得S△ABC=5S△AEF,再证明
则易得S△ABC=5S△AEF,再证明![]() 然后根据相似三角形的性质得到
然后根据相似三角形的性质得到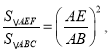 再利用勾股定理求出AB即可得到AE的长;
再利用勾股定理求出AB即可得到AE的长;
(2)①通过证明四条边相等判断四边形AEMF为菱形;
②连结AM交EF于点O,如图②,设![]() 则
则![]() 先证明
先证明![]() 得到
得到![]() 解出
解出![]() 后计算出
后计算出![]() 再利用勾股定理计算出AM,然后根据菱形的面积公式计算EF;
再利用勾股定理计算出AM,然后根据菱形的面积公式计算EF;
(3)如图③,作作![]() 于H,先证明
于H,先证明![]() 利用相似比得到
利用相似比得到![]() 设
设![]() ,则
,则![]()
![]() 再证明
再证明![]() 利用相似比可计算出
利用相似比可计算出![]() 则可计算出
则可计算出![]() 和
和![]() ,接着利用勾股定理计算出
,接着利用勾股定理计算出![]() ,从而得到
,从而得到![]() 的长,于是可计算出
的长,于是可计算出![]() 的值.
的值.
试题解析:(1)∵![]() 的一角沿EF折叠,折叠后点A落在AB边上的点D处,
的一角沿EF折叠,折叠后点A落在AB边上的点D处,
∴![]() ,
, ![]() ≌
≌![]() ,
,
∴![]()
∵S四边形ECBF=![]()
∴S△ABC=5S△AEF,
在Rt ![]() 中,∵
中,∵![]()
∴![]()
∵![]()
∴![]()
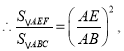
即![]()
∴![]()
由折叠知, ![]()
(2)①连结AM交EF于点O,如图2,

∵![]() 的一角沿EF折叠,折叠后点A落在AB边上的点D处,
的一角沿EF折叠,折叠后点A落在AB边上的点D处,
∴![]()
∵MF∥AC,
∴![]()
∴![]()
∴![]()
∴![]()
∴四边形AEMF为菱形,
②设![]() 则
则![]()
∵四边形AEMF为菱形,
∴EM∥AB,
∴![]()
∴![]()
即![]()
解得![]()
在Rt ![]() 中,
中, ![]()
∵S菱形AEMF![]()
∴![]()
(3)如图③,作![]() 于H,
于H,
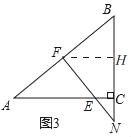
∵EC∥FH,
∴![]()
∴![]()
∴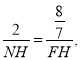
∴![]()
设![]() ,则
,则![]()
![]()
∵FH∥AC,
∴![]()
∴![]()
![]()
∴![]()
∴![]()
在Rt ![]() 中,
中, ![]()
∴![]()
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克)
50
60
70
销售量y(千克)
100
80
60
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),则当售价x定为多少元时,厂商每天能获得最大利润?最大利润是多少?
(3)如果超市要获得每天不低于1350元的利润,且符合超市自己的规定,那么该商品每千克售价的取值范围是多少?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若点A在数轴上对应的数为a,点B在数轴上对应的数为b,点C在数轴上对应的数为c,且|a+2|+(b﹣1)2=0,2c﹣1=
 c+2.
c+2.
(1)求线段AB的长;
(2)在数轴上是否存在点P,使得PA+PB=PC?若存在,求出点P对应的数;若不存在,说明理由.
(3)现在点A,B,C开始在数轴上运动,若点A以每秒1个单位长度向左运动,同时,点B和点C分别以每秒4个单位长度和9个单位长度的速度向右运动.假设t秒后,点B和点C之间的距离表示为BC,点A和点B之间的距离表示为AB.请问AB﹣BC的值是否随着时间t的变化而变化?若变化,请说明理由;若不变,请求出常数值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在研究反比例函数y=﹣
 的图象时,我们发现有如下性质:
的图象时,我们发现有如下性质:(1)y=﹣
 的图象是中心对称图形,对称中心是原点.
的图象是中心对称图形,对称中心是原点.(2)y=﹣
 的图象是轴对称图形,对称轴是直线y=x,y=﹣x.
的图象是轴对称图形,对称轴是直线y=x,y=﹣x.(3)在x<0与x>0两个范围内,y随x增大而增大;
类似地,我们研究形如:y=﹣
 +3的函数:
+3的函数:(1)函数y=﹣
 +3图象是由反比例函数y=﹣
+3图象是由反比例函数y=﹣ 图象向____平移______个单位,再向_______平移______个单位得到的.
图象向____平移______个单位,再向_______平移______个单位得到的.(2)y=﹣
 +3的图象是中心对称图形,对称中心是______.
+3的图象是中心对称图形,对称中心是______.(3)该函数图象是轴对称图形吗?如果是,请求出它的对称轴,如果不是,请说明理由.
(4)对于函数y=
 ,x在哪些范围内,y随x的增大而增大?
,x在哪些范围内,y随x的增大而增大? -
科目: 来源: 题型:
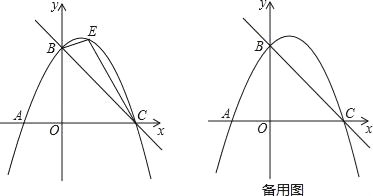
查看答案和解析>>【题目】如图,直线y=﹣
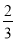 x+4与x轴交于点C,与y轴交于点B,抛物线y=ax2+
x+4与x轴交于点C,与y轴交于点B,抛物线y=ax2+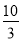 x+c经过B、C两点.
x+c经过B、C两点.(1)求抛物线的解析式;
(2)如图,点E是直线BC上方抛物线上的一动点,当△BEC面积最大时,请求出点E的坐标;
(3)在(2)的结论下,过点E作y轴的平行线交直线BC于点M,连接AM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于反比例函数
 ,下列说法中不正确的是( )
,下列说法中不正确的是( )A. 图像经过点(1.-2)
B. 图像分布在第二第四象限
C. x>0时,y随x增大而增大
D. 若点A(
 )B(
)B( )在图像上,若
)在图像上,若 ,则
,则
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图两张长相等,宽分别是1和3的矩形纸片上叠合在一起,重叠部分为四边形ABCD,且AB+BC=6,则四面行ABCD的面积为( )

A. 3B.
 C. 9D.
C. 9D. 
相关试题

