【题目】已知:如图①,长方形ABCD中,E是边AD上一点,且AE=6cm,点P从B出发,沿折线BE-ED-DC匀速运动,运动到点C停止.P的运动速度为2cm/s,运动时间为t(s),△BPC的面积为y(cm2),y与t的函数关系图象如图②,则下列结论正确的有( )
①a=7 ②AB=8cm ③b=10 ④当t=10s时,y=12cm2 
A. 1个B. 2个C. 3个D. 4个
参考答案:
【答案】B
【解析】
先通过t=5,y=40计算出AB长度和BC长度,则DE长度可求,根据BE+DE长计算a的值,b的值是整个运动路程除以速度即可,当t=10时找到P点位置计算△BPC面积即可判断y值.
解:当P点运动到E点时,△BPC面积最大,结合函数图象可知当t=5时,△BPC面积最大为40,
∴BE=5×2=10.
在Rt△ABE中,利用勾股定理可得AB=8,
又![]() ,所以BC=10.
,所以BC=10.
则ED=10-6=4.当P点从E点到D点时,所用时间为4÷2=2s,∴a=5+2=7.
故①和②都正确;
P点运动完整个过程需要时间t=(10+4+8)÷2=11s,即b=11,③错误;
当t=10时,P点运动的路程为10×2=20cm,此时PC=22-20=2,
△BPC面积为![]() ×10×2=10cm2,④错误.
×10×2=10cm2,④错误.
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小红用110根长短相同的小木棍按照如图所示的方式,连续摆正方形或六边形,要求相邻的图形只有一条公共边.
(1)小红首先用
 根小木棍摆出了
根小木棍摆出了 个小正方形,请你用等式表示
个小正方形,请你用等式表示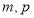 之间的关系: ;
之间的关系: ;(2)小红用剩下的小木棍摆出了一些六边形,且没有木棍剩余.已知他摆出的正方形比六边形多4个,请你求出摆放的正方形和六边形各多少个?
(3)小红重新用50根小木棍,摆出了
 排,共
排,共 个小正方形.其中每排至少含有1个小正方形,每排含有的小正方形的个数可以不同.请你用等式表示
个小正方形.其中每排至少含有1个小正方形,每排含有的小正方形的个数可以不同.请你用等式表示 之间的关系,并写出所有
之间的关系,并写出所有 可能的取值.
可能的取值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y1=x+b与双曲线y2=
 交于点A(1,4)和点B,经过点A的另一条直线与双曲线y2=
交于点A(1,4)和点B,经过点A的另一条直线与双曲线y2= 交于点C.则:
交于点C.则:①直线AB的解析式为y1=x+3;
②B(﹣1,﹣4);
③当x>1时,y2<y1;
④当AC的解析式为y=4x时,△ABC是直角三角形.
其中正确的是 .(把所有正确结论的序号都写在横线上)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
 ,
, 分别是直线
分别是直线 上的点.
上的点.(1)在图1中,判断
 和
和 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;(2)在图2中,请你直接写出
 和
和 之间的数量关系(不需要证明);
之间的数量关系(不需要证明);(3)在图3中,
 平分
平分 ,
, 平分
平分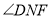 ,且
,且 ,求
,求 的度数.
的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】水果种植大户小方,为了吸引更多的顾客,组织了观光采摘游活动.每一位来采摘水果的顾客都有一次抽奖机会:在一只不透明的盒子里有A,B,C,D四张外形完全相同的卡片,抽奖时先随机抽出一张卡片,再从盒子中剩下的3张中随机抽取第二张.
(1)请利用树状图(或列表)的方法,表示前后两次抽得的卡片所有可能的情况;
(2)如果抽得的两张卡片是同一种水果图片就可获得奖励,那么得到奖励的概率是多少?

A B C D
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C是AB延长线上一点,CD与⊙O相切于点E,AD⊥CD于点D.

(1)求证:AE平分∠DAC;
(2)若AB=4,∠ABE=60°.
①求AD的长;
②求出图中阴影部分的面积.
-
科目: 来源: 题型:
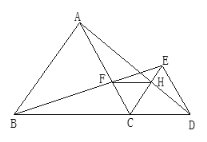
查看答案和解析>>【题目】如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,
(1)求证:△BCE≌△ACD;
(2)求证:FC=HC
(3)求证:FH∥BD.
相关试题

