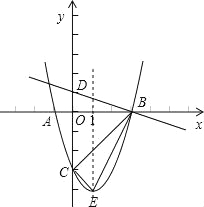
【题目】如图,抛物线y=ax2+bx﹣3(a≠0)的顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且BO=OC=3AO,直线y=﹣![]() x+1与y轴交于点D.
x+1与y轴交于点D.
(1)求抛物线的解析式;
(2)证明:△DBO∽△EBC;
(3)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的P点坐标,若不存在,请说明理由.
参考答案:
【答案】(1)y=x2﹣2x﹣3;(2)详见解析;(3)符合条件的P点坐标为P(1,﹣1)或P(1,![]() )或P(1,﹣
)或P(1,﹣![]() )或P(1,﹣3+
)或P(1,﹣3+![]() )或P(1,﹣3﹣
)或P(1,﹣3﹣![]() ).
).
【解析】
试题分析:(1)先求出点C的坐标,在由BO=OC=3AO,确定出点B,A的坐标,最后用待定系数法求出抛物线解析式;(2)先求出点A,B,C,D,E的坐标,从而求出BC=3![]() ,BE=2
,BE=2![]() ,CE=
,CE=![]() ,OD=1,OB=3,BD=
,OD=1,OB=3,BD=![]() ,求出比值,得到
,求出比值,得到![]() 得出结论;(3)设出点P的坐标,表示出PB,PC,求出BC,分三种情况计算即可.
得出结论;(3)设出点P的坐标,表示出PB,PC,求出BC,分三种情况计算即可.
试题解析:(1)∵抛物线y=ax2+bx﹣3,
∴c=﹣3,
∴C(0,﹣3),
∴OC=3,
∵BO=OC=3AO,
∴BO=3,AO=1,
∴B(3,0),A(﹣1,0),
∵该抛物线与x轴交于A、B两点,
∴![]() ,
,
∴![]() ,
,
∴抛物线解析式为y=x2﹣2x﹣3,
(2)由(1)知,抛物线解析式为y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴E(1,﹣4),
∵B(3,0),A(﹣1,0),C(0,﹣3),
∴BC=3![]() ,BE=2
,BE=2![]() ,CE=
,CE=![]() ,
,
∵直线y=﹣![]() x+1与y轴交于点D,
x+1与y轴交于点D,
∴D(0,1),
∵B(3,0),
∴OD=1,OB=3,BD=![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴△BCE∽△BDO,
(3)存在,
理由:设P(1,m),
∵B(3,0),C(0,﹣3),
∴BC=3![]() ,PB=
,PB=![]() ,PC=
,PC=![]() ,
,
∵△PBC是等腰三角形,
①当PB=PC时,
∴![]() =
=![]() ,
,
∴m=﹣1,
∴P(1,﹣1),
②当PB=BC时,
∴3![]() =
=![]() ,
,
∴m=±![]() ,
,
∴P(1,![]() )或P(1,﹣
)或P(1,﹣![]() ),
),
③当PC=BC时,
∴3![]() =
=![]() ,
,
∴m=﹣3±![]() ,
,
∴P(1,﹣3+![]() )或P(1,﹣3﹣
)或P(1,﹣3﹣![]() ),
),
∴符合条件的P点坐标为P(1,﹣1)或P(1,![]() )或P(1,﹣
)或P(1,﹣![]() )或P(1,﹣3+
)或P(1,﹣3+![]() )或P(1,﹣3﹣
)或P(1,﹣3﹣![]() ).
).
考点:二次函数的综合题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折叠长方形纸片的一边AD,使点D落在BC边上的点F处,已知BC=10cm,AB=8cm,求EC的长。

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店四月份的利润为6.3万元,此后两个月进入淡季,利润均以相同的百分比下降,至六月份利润为5.4万元.设下降的百分比为x,由题意列出方程 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题(共18分)
(1)(﹣8)﹣(+4)+(﹣6)﹣(﹣1)
(2)﹣2﹣1+(﹣16)﹣(﹣13);
(3)
 ;
;(4)

(5)
 (用简便方法计算);
(用简便方法计算);(6)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知△OAB、△OBC、△OCD、△ODE、△OEF和△OFA均为边长为a的等边三角形,点P为边BC上任意一点,过P作PM∥AB交AF于M,作PN∥CD交DE于N.

(1)那么∠MPN=______,并求证PM+PN=3a;
(2)如图2,联结OM、ON.求证:OM=ON;
(3)如图3,OG平分∠MON,判断四边形OMGN是否为特殊四边形,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(x+2,2y﹣4)关于x轴的对称点是(4,﹣2),则x+y=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b互为相反数,c,d互为倒数,则﹣5a+2017cd﹣5b=_____.
相关试题

