搜索
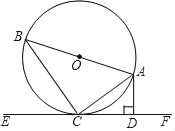
【题目】已知：如图AB是⊙O的直径，AC是弦，直线EF是过点C的⊙O的切线，AD⊥EF于点D．
（1）求证：∠BAC=∠CAD；
（2）若∠B=30°，AB=12，求AC的长．
参考答案：
【答案】(1)见解析 (2)6
【解析】试题分析：（1）连接OC，利用切线和半径OA=OB构成的等腰三角形可以得到∠BAC=∠CAD；(2) 特殊直角三角形，30°对应的边是斜边一半.
试题解析：
（1）证明：连接OC，如图，
∵DE为切线，
∴OC⊥DE，
而AD⊥EF，
∴OC∥AD，
∴∠OCA=∠CAD，
∵OA=OC，
∴∠BAC=∠OCA，
∴∠BAC=∠CAD；
（2）解：∵AB为直径，
∴∠ACB=90°，
在Rt△ABC中，∵∠B=30°，
∴AC=
AB=
×12=6．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在一条笔直的公路上有A、B、C三地，C地位于A、B两地之间，甲车从A地沿这条公路匀速驶向C地，乙车从B地沿这条公路匀速驶向A地，在甲车出发至甲车到达C地的过程中，甲、乙两车各自与C地的距离y（km）与甲车行驶时间t（h）之间的函数关系如图所示．下列结论：①甲车出发2h时，两车相遇；②乙车出发1.5h时，两车相距170km；③乙车出发
h时，两车相遇；④甲车到达C地时，两车相距40km．其中正确的是______（填写所有正确结论的序号）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】借助一副三角板，可以得到一些平面图形
（1）如图1，∠AOC＝ 度．由射线OA，OB，OC组成的所有小于平角的和是多少度？
（2）如图2，∠1的度数比∠2度数的3倍还多30°，求∠2的度数；
（3）利用图3，反向延长射线OA到M，OE平分∠BOM，OF平分∠COM，请按题意补全图（3），并求出∠EOF的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】
朗读者
自开播以来，以其厚重的文化底蕴和感人的人文情怀，感动了数以亿计的观众，岳池县某中学开展“朗读”比赛活动，九年级
、
班根据初赛成绩，各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩
满分为100分
如图所示．平均数
中位数
众数
九
班85
85
九
班80
根据图示填写表格；结合两班复赛成绩的平均数和中位数，分析哪个班级的复赛成绩较好；
如果规定成绩较稳定班级胜出，你认为哪个班级能胜出？说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，过点C（1，3）、D（3，1）分别作x轴的垂线，垂足分别为A、B．
（1）求直线CD和直线OD的解析式；
（2）点M为直线OD上的一个动点，过M作x轴的垂线交直线CD于点N，是否存在这样的点M，使得以A、C、M、N为顶点的四边形为平行四边形？若存在，求此时点M的横坐标；若不存在，请说明理由；
（3）若△AOC沿CD方向平移（点C在线段CD上，且不与点D重合），在平移的过程中，设平移距离为
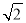t，△AOC与△OBD重叠部分的面积记为s，试求s与t的函数关系式．
-
科目： 来源： 题型：
查看答案和解析>>【题目】“岳池米粉”是四川岳池的传统特色小吃之一，距今有三百多年的历史，为了将本地传统小吃推广出去，县领导组织20辆汽车装运A，B，C三种不同品种的米粉42 t到外地销售，按规定每辆车只装同一品种米粉，且必须装满，每种米粉不少于2车.
米粉品种
A
B
C
每辆汽车运载量/t
2.2
2.1
2
每吨米粉获利/元
600
800
500
(1)设用x辆车装运A种米粉，用y辆车装运B种米粉，根据上表提供的信息，求y与x的函数关系式，并求x的取值范围；
(2)设此次外售活动的利润为w元，求w与x的函数关系式以及最大利润，并安排相应的车辆分配方案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，某长方形广场的四角都有一块半径相同的
圆形的草地，已知圆形的半径为r米，长方形的长为a米，宽为b米．（1）请列式表示广场空地的面积；
（2）若长方形的长为300米，宽为200米，圆形的半径为10米，计算广场空地的面积（计算结果保留π）．
相关试题
