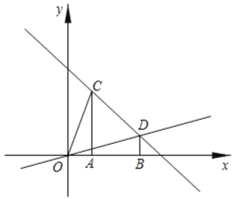
【题目】在平面直角坐标系中,过点C(1,3)、D(3,1)分别作x轴的垂线,垂足分别为A、B.
(1)求直线CD和直线OD的解析式;
(2)点M为直线OD上的一个动点,过M作x轴的垂线交直线CD于点N,是否存在这样的点M,使得以A、C、M、N为顶点的四边形为平行四边形?若存在,求此时点M的横坐标;若不存在,请说明理由;
(3)若△AOC沿CD方向平移(点C在线段CD上,且不与点D重合),在平移的过程中,设平移距离为![]() t,△AOC与△OBD重叠部分的面积记为s,试求s与t的函数关系式.
t,△AOC与△OBD重叠部分的面积记为s,试求s与t的函数关系式.
参考答案:
【答案】(1)直线OD的解析式为y=![]() x;(2)存在.满足条件的点M的横坐标
x;(2)存在.满足条件的点M的横坐标![]() 或
或![]() ,理由见解析;(3)S=﹣
,理由见解析;(3)S=﹣![]() (t﹣1)2+
(t﹣1)2+![]() .
.
【解析】
(1)理由待定系数法即可解决问题;
(2)如图,设M(m,![]() m),则N(m,-m+4).当AC=MN时,A、C、M、N为顶点的四边形为平行四边形,可得|-m+4-
m),则N(m,-m+4).当AC=MN时,A、C、M、N为顶点的四边形为平行四边形,可得|-m+4-![]() m|=3,解方程即可;
m|=3,解方程即可;
(3)如图,设平移中的三角形为△A′O′C′,点C′在线段CD上.设O′C′与x轴交于点E,与直线OD交于点P;设A′C′与x轴交于点F,与直线OD交于点Q.根据S=S△OFQ-S△OEP=![]() OFFQ-
OFFQ-![]() OEPG计算即可;
OEPG计算即可;
(1)设直线CD的解析式为y=kx+b,则有![]() ,解得
,解得![]() ,
,
∴直线CD的解析式为y=﹣x+4.
设直线OD的解析式为y=mx,则有3m=1,m=![]() ,
,
∴直线OD的解析式为y=![]() x.
x.
(2)存在.
理由:如图,设M(m,![]() m),则N(m,﹣m+4).
m),则N(m,﹣m+4).
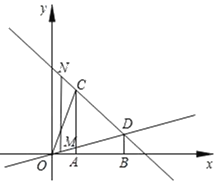
当AC=MN时,A、C、M、N为顶点的四边形为平行四边形,
∴|﹣m+4﹣![]() m|=3,
m|=3,
解得m=![]() 或
或![]() ,
,
∴满足条件的点M的横坐标![]() 或
或![]() .
.
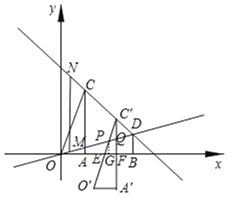
(3)如图,设平移中的三角形为△A′O′C′,点C′在线段CD上.
设O′C′与x轴交于点E,与直线OD交于点P;
设A′C′与x轴交于点F,与直线OD交于点Q.
因为平移距离为![]() t,所以水平方向的平移距离为t(0≤t<2),
t,所以水平方向的平移距离为t(0≤t<2),
则图中AF=t,F(1+t,0),Q(1+t,![]() +
+![]() t),C′(1+t,3﹣t).
t),C′(1+t,3﹣t).
设直线O′C′的解析式为y=3x+b,
将C′(1+t,3﹣t)代入得:b=﹣4t,
∴直线O′C′的解析式为y=3x﹣4t.
∴E(![]() t,0).
t,0).
联立y=3x﹣4t与y=![]() x,解得x=
x,解得x=![]() t,
t,
∴P(![]() t,
t,![]() t).
t).
过点P作PG⊥x轴于点G,则PG=![]() t.
t.
∴S=S△OFQ﹣S△OEP=![]() OFFQ﹣
OFFQ﹣![]() OEPG
OEPG
=![]() (1+t)(
(1+t)(![]() +
+![]() t)﹣
t)﹣![]()
![]() t
t![]() t
t
=﹣![]() (t﹣1)2+
(t﹣1)2+![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】借助一副三角板,可以得到一些平面图形
(1)如图1,∠AOC= 度.由射线OA,OB,OC组成的所有小于平角的和是多少度?
(2)如图2,∠1的度数比∠2度数的3倍还多30°,求∠2的度数;
(3)利用图3,反向延长射线OA到M,OE平分∠BOM,OF平分∠COM,请按题意补全图(3),并求出∠EOF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】
 朗读者
朗读者 自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级
自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级 、
、 班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩
班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩 满分为100分
满分为100分 如图所示.
如图所示.平均数
中位数
众数
九
 班
班85
85
九
 班
班80
 根据图示填写表格;
根据图示填写表格; 结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好; 如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.
如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.
-
科目: 来源: 题型:
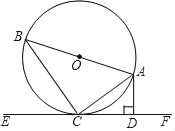
查看答案和解析>>【题目】已知:如图AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.
(1)求证:∠BAC=∠CAD;
(2)若∠B=30°,AB=12,求AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“岳池米粉”是四川岳池的传统特色小吃之一,距今有三百多年的历史,为了将本地传统小吃推广出去,县领导组织20辆汽车装运A,B,C三种不同品种的米粉42 t到外地销售,按规定每辆车只装同一品种米粉,且必须装满,每种米粉不少于2车.
米粉品种
A
B
C
每辆汽车运载量/t
2.2
2.1
2
每吨米粉获利/元
600
800
500
(1)设用x辆车装运A种米粉,用y辆车装运B种米粉,根据上表提供的信息,求y与x的函数关系式,并求x的取值范围;
(2)设此次外售活动的利润为w元,求w与x的函数关系式以及最大利润,并安排相应的车辆分配方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某长方形广场的四角都有一块半径相同的
 圆形的草地,已知圆形的半径为r米,长方形的长为a米,宽为b米.
圆形的草地,已知圆形的半径为r米,长方形的长为a米,宽为b米.(1)请列式表示广场空地的面积;

(2)若长方形的长为300米,宽为200米,圆形的半径为10米,计算广场空地的面积(计算结果保留π).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题6分)甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
相关试题

