【题目】如图,一次函数 ![]() 分别交y轴、x 轴于A、B两点,抛物线
分别交y轴、x 轴于A、B两点,抛物线 ![]() 过A、B两点.
过A、B两点.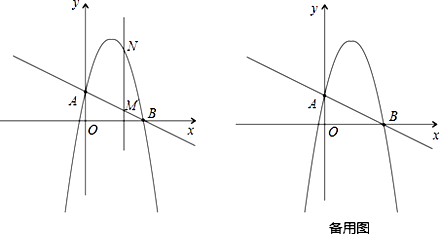
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于点M,交这个抛物线于点N.求当t 取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
参考答案:
【答案】
(1)解:∵ ![]() 分别交y轴、x轴于A.、B两点,
分别交y轴、x轴于A.、B两点,
∴A、B点的坐标为:A(0,2),B(4,0),
将x=0,y=2代入y=x+bx+c得c=2,
将x=4,y=0,c=2代入y=x+bx+c得0=16+4b+2,解得b= ![]() ,
,
∴抛物线解析式为: ![]()
(2)解:如图1,
由题意可知,直线MN即是直线 ![]() ,
,
∵点M在直线 ![]() 上,点N在抛物线
上,点N在抛物线 ![]() 上,
上,
∴点M、N的坐标分别为 ![]() 、
、 ![]() ,
,
∵在第一象限中,点N在点M的上方,
∴MN= ![]() ,
,
∴当 ![]() 时,MN最长=4;
时,MN最长=4;
(3)解:由(2)可知,A(0,2),M(2,1),N(2,5).
以A. M、N、D为顶点作平行四边形,D点的可能位置有三种情形,如图2所示: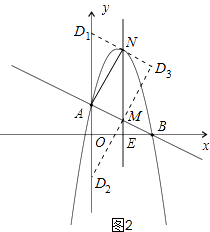
(i)当D在y轴上时,设D的坐标为(0,a)
由AD=MN,得|a2|=4,解得a1=6,a2=2,
从而D1为(0,6)或D2(0,2),
(ii)当D不在y轴上时,由图可知D3为D1N与D2M的交点,
由D1、D2、M、N的坐标可求得直线D1N的解析式为:y= ![]() x+6,直线D2M的解析式为:y=
x+6,直线D2M的解析式为:y= ![]() x2,
x2,
由 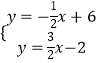 解得
解得 ![]() ,
,
∴D3的坐标为:(4,4),
综上所述,所求的D点坐标为(0,6),(0,2)或(4,4)
【解析】(1)先求出直线y=-![]() x+2与x轴、y轴的交点B、A的坐标,再将点A、B的坐标分别代入二次函数解析式,建立方程求出b、c的值,就可得出二次函数解析式。
x+2与x轴、y轴的交点B、A的坐标,再将点A、B的坐标分别代入二次函数解析式,建立方程求出b、c的值,就可得出二次函数解析式。
(2)根据直线x=t,在第一象限交直线AB于点M,交这个抛物线于点N,可知点M、N的横坐标都为t,根据两函数解析式可得出两点的纵坐标,再根据MN=点N的纵坐标-点M的纵坐标,列出MN关于t的函数解析式,求出顶点坐标,即可得到MN有最大值时t的值即MN的长。
(3)抓住已知条件在(2)的情况下MN=4,要以A、M、N、D为顶点作平行四边形,根据点D的位置情况分两种:当(i)当D在y轴上时,设D的坐标为(0,a),根据MN=4即|a2|=4,求出a的值,得到点D的坐标由两个;(ii)当D不在y轴上时,即是以MN为平行四边形的对角线时,可知D3为D1N与D2M的交点,再求出直线D1N的解析式和直线D2M的解析式,然后将两一次函数解析式联立方程组求解即可得出点D的坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】研究“掷一枚图钉,钉尖朝上”的概率,两个小组用同一个图钉做试验进行比较,他们的统计数据如下:
掷图钉的次数
50
100
200
300
400
钉尖朝上
的次数
第一小组
23
39
79
121
160
第二小组
24
41
81
124
164
(1)请你估计第一小组和第二小组所得的概率分别是多少?
(2)你认为哪一个小组的结果更准确?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△
 的位置,点B,O分别落在点
的位置,点B,O分别落在点  ,
,  处,点
处,点  在
在  轴上,再将△
轴上,再将△ 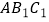 绕点
绕点  顺时针旋转到△
顺时针旋转到△  的位置,点
的位置,点  在
在  轴上,将△
轴上,将△  绕点
绕点  顺时针旋转△
顺时针旋转△  的位置,点
的位置,点  在
在  轴上……依次进行下去。若点
轴上……依次进行下去。若点  ,B(0,2),则点
,B(0,2),则点  的坐标为 .
的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】乘法公式的探究及应用.
(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式);
(3)比较图1、图2两图的阴影部分面积,可以得到乘法公式 (用式子表达);
(4)运用你所得到的公式,计算下列各题:
①(2m+n-p)(2m-n+p);②10.3×9.7.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:CD是经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α.

(1)若直线CD经过∠BCA的内部,且E,F在射线CD上.
①如图1,若∠BCA=90°,∠α=90°,则BE CF;
②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件 ,使①中的结论仍然成立,并说明理由;
(2)如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出关于EF,BE,AF三条线段数量关系的合理猜想:
-
科目: 来源: 题型:
查看答案和解析>>【题目】以点A为顶点作两个等腰直角三角形(△ABC,△ADE),如图1所示放置,使得一直角边重合,连接BD,CE.

(1)说明BD=CE;
(2)延长BD,交CE于点F,求∠BFC的度数;
(3)若如图2放置,上面的结论还成立吗?请简单说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,AB//EG//x轴,BC//DE//HG//AP//y轴,点D、C、P、H在x轴上,A(1,2),B(-1,2),D(-3,0),E(-3,-2),G(3,-2),把一条长为2019个单位长度且没有弹性的细线(粗细忽略不计)的一端固定在点A处,并按A-B-C-D-E-F-G-H-P-A…的规律紧绕在图形“凸”的边上,则细线另一端所在位置的点的坐标是( )

A.(1,2)B.(-1,2)C.(-1,-2)D.(1,1)
相关试题

