【题目】以点A为顶点作两个等腰直角三角形(△ABC,△ADE),如图1所示放置,使得一直角边重合,连接BD,CE.

(1)说明BD=CE;
(2)延长BD,交CE于点F,求∠BFC的度数;
(3)若如图2放置,上面的结论还成立吗?请简单说明理由.
参考答案:
【答案】(1)见解析;(2)90°;(3)成立,见解析
【解析】
试题分析:(1)根据等腰直角三角形的性质得到AB=AC,∠BAD=∠EAC=90°,AD=AE,利用“SAS”可证明△ADB≌△AEC,则BD=CE;
(2)由△ADB≌△AEC得到∠ACE=∠DBA,利用三角形内角和定理可得到∠BFC=180°﹣∠ACE﹣∠CDF=180°﹣∠DBA﹣∠BDA=∠DAB=90°;
(3)与(1)一样可证明△ADB≌△AEC,得到BD=CE,∠ACE=∠DBA,利用三角形内角和定理得到∠BFC=∠CAB=90°.
解:(1)∵△ABC、△ADE是等腰直角三角形,
∴AB=AC,∠BAD=∠EAC=90°,AD=AE,
∵在△ADB和△AEC中,
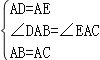 ,
,
∴△ADB≌△AEC(SAS),
∴BD=CE;
(2)∵△ADB≌△AEC,
∴∠ACE=∠ABD,
而在△CDF中,∠BFC=180°﹣∠ACE﹣∠CDF
又∵∠CDF=∠BDA
∴∠BFC=180°﹣∠DBA﹣∠BDA
=∠DAB
=90°;
(3)BD=CE成立,且两线段所在直线互相垂直,即∠BFC=90°.理由如下:
∵△ABC、△ADE是等腰直角三角形
∴AB=AC,AD=AE,∠BAC=∠EAD=90°,
∵∠BAC+∠CAD=∠EAD+∠CAD
∴∠BAD=∠CAE,
∵在△ADB和△AEC中,
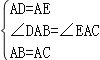 ,
,
∴△ADB≌△AEC(SAS)
∴BD=CE,∠ACE=∠DBA,
∴∠BFC=∠CAB=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在矩形ABCD中,BC=2CD=2a,点E在边CD上,在矩形ABCD的左侧作矩形ECGF,使CG=2GF=2b,连接BD,CF,连结AF交BD于点H.
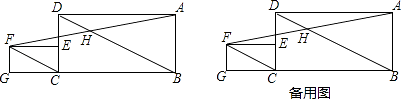
(1)求证:BD∥CF;
(2)求证:H是AF的中点;
(3)连结CH,若HC⊥BD,求a:b的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2( ),
且∠1=∠4( )
∴∠2=∠4(等量代换)
∴CE∥BF( )
∴∠ =∠3( )
又∵∠B=∠C(已知)
∴∠3=∠B( )
∴AB∥CD( ).

-
科目: 来源: 题型:
查看答案和解析>>【题目】小凡与小光从学校出发到距学校5千米的图书馆看书,小光直接去图书馆, 小凡途中从路边超市买了一些学习用品,如图反应了他们俩人离开学校的路程s(千米)与时间t(分钟)的关系,请根据图象提供的信息回答问题:
(1) 是描述小凡的运动过程(填
 或
或 );
);(2)小凡和小光先出发的是 ,先出发了 分钟;
(3)小凡与小光先到达图书馆的是 ,先到了 分钟;
(4)求小凡与小光从学校到图书馆的平均速度各是多少?(不包括中间停留的时间)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,DC=12,AD=13,求四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A、B、C的坐标分别为(-1,3)、(-4,1)、(-2,1),将△ABC沿一确定方向平移得到△A1B1C1,点B的对应点B1的坐标是(1,2),则点A1,C1的坐标分别是( )
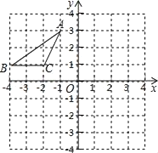
A.A1(4,4),C1(3,2)B.A1(3,3),C1(2,1)
C.A1(4,3),C1(2,3)D.A1(3,4),C1(2,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两张宽度相等的纸条叠放在一起,重叠部分构成四边形ABCD.
(1)求证:四边形ABCD是菱形;
(2)若纸条宽3cm,∠ABC=60°,求四边形ABCD的面积.

相关试题

