【题目】乘法公式的探究及应用.
(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式);
(3)比较图1、图2两图的阴影部分面积,可以得到乘法公式 (用式子表达);
(4)运用你所得到的公式,计算下列各题:
①(2m+n-p)(2m-n+p);②10.3×9.7.

参考答案:
【答案】(1)a2 -b2;(2)a-b,a+b,(a+b)(a-b);(3)(a+b)(a﹣b)=a2 ﹣b2;(4)①4m2 -n2 +2np-p2;②99.91.
【解析】
(1)利用面积公式:大正方形的面积-小正方形的面积=阴影面积;
(2)根据图1可得矩形的长和宽,然后利用矩形面积公式进行求解即可;
(3)利用面积相等列出等式即可;
(4)①先分组,然后利用平方差公式简便计算即可;
②写成两个数的和与两个数的差的形式,然后利用平方差公式简便计算即可.
(1)利用正方形的面积公式可知:阴影部分的面积=a2 -b2,
故答案为:a2 -b2;
(2)由图可知矩形的宽是a-b,长是a+b,面积是(a+b)(a-b),
故答案为:a-b,a+b,(a+b)(a-b);
(3)由阴影部分的面积不变可得(a+b)(a﹣b)=a2 ﹣b2,
故答案为:(a+b)(a﹣b)=a2 ﹣b2;
(4)①原式=[2m+(n-p)][2m-(n-p)] =(2m)2 -(n-p)2 =4m2 -n2 +2np-p2;
②原式=(10+0.3)×(10-0.3)=102 -0.32=100-0.09=99.91.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图中,用数字表示的∠1、∠2、∠3、∠4各角中,错误的判断是( )

A. 若将AC作为第三条直线,则∠1和∠3是同位角
B. 若将AC作为第三条直线,则∠2和∠4是内错角
C. 若将BD作为第三条直线,则∠2和∠4是内错角
D. 若将CD作为第三条直线,则∠3和∠4是同旁内角
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线经过A(1,0),B(4,0),C(0,﹣4)三点,点D是直线BC上方的抛物线上的一个动点,连结DC,DB,则△BCD的面积的最大值是( )
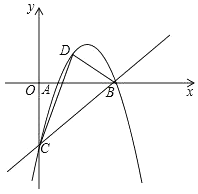
A.7
B.7.5
C.8
D.9 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线a,b被直线c,d所截,直线a,c,d相交于点O,按要求完成下列各小题.
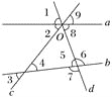
(1)在图中的∠1~∠9这9个角中,同位角共有多少对?请你全部写出来;
(2)∠4和∠5是什么位置关系的角?∠6和∠8之间的位置关系与∠4和∠5的相同吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解全区5000名初中毕业生的体重情况,随机抽测了400名学生的体重,频率分布如图所示(每小组数据可含最小值,不含最大值),其中从左至右前四个小长方形的高依次为0.02、0.03、0.04、0.05,由此可估计全区初中毕业生的体重不小于60千克的学生人数约为人.
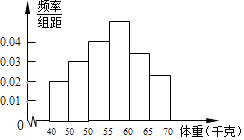
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A,B两点的坐标分别为(2
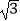 ,0),(0,10),M是△AOB外接圆⊙C上的一点,且∠AOM=30°,则点M的坐标为 .
,0),(0,10),M是△AOB外接圆⊙C上的一点,且∠AOM=30°,则点M的坐标为 . 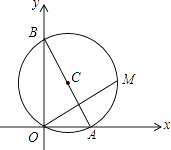
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OM⊥AB.
(1)若∠1=∠2,求∠NOD.
(2)若∠1=
 ∠BOC,求∠AOC与∠MOD.
∠BOC,求∠AOC与∠MOD.
相关试题

