搜索
【题目】如图，在平面直角坐标系中，AB//EG//x轴，BC//DE//HG//AP//y轴，点D、C、P、H在x轴上，A(1，2)，B(-1，2)，D(-3，0)，E(-3，-2)，G(3，-2)，把一条长为2019个单位长度且没有弹性的细线（粗细忽略不计）的一端固定在点A处，并按A-B-C-D-E-F-G-H-P-A…的规律紧绕在图形“凸”的边上，则细线另一端所在位置的点的坐标是（ ）
A.(1，2)B.(-1，2)C.(-1，-2)D.(1，1)
参考答案：
【答案】D
【解析】
先求出“凸”形ABCDEFGHP的周长为20，得到2019÷20的余数，进而可得答案．
解：∵A（1，2），B（﹣1，2），D（﹣3，0），E（﹣3，﹣2），G（3，﹣2），
∴“凸”形ABCDEFGHP的周长为20，
∵2019÷20的余数为19，
∴细线另一端所在位置的点在P处上面1个单位的位置，坐标为（1，1）．
故选：D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数
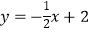分别交y轴、x 轴于A、B两点，抛物线 
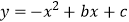过A、B两点.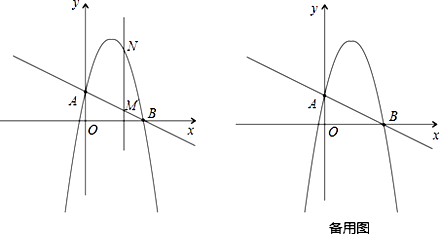
（1）求这个抛物线的解析式；
（2）作垂直x轴的直线x=t，在第一象限交直线AB于点M，交这个抛物线于点N.求当t 取何值时，MN有最大值？最大值是多少？
（3）在（2）的情况下，以A、M、N、D为顶点作平行四边形，求第四个顶点D的坐标. -
科目： 来源： 题型：
查看答案和解析>>【题目】已知：CD是经过∠BCA顶点C的一条直线，CA＝CB．E，F分别是直线CD上两点，且∠BEC＝∠CFA＝∠α．
(1)若直线CD经过∠BCA的内部，且E，F在射线CD上．
①如图1，若∠BCA＝90°，∠α＝90°，则BE CF；
②如图2，若0°＜∠BCA<180°，请添加一个关于∠α与∠BCA关系的条件 ，使①中的结论仍然成立，并说明理由；
(2)如图3，若直线CD经过∠BCA的外部，∠α＝∠BCA，请提出关于EF，BE，AF三条线段数量关系的合理猜想：
-
科目： 来源： 题型：
查看答案和解析>>【题目】以点A为顶点作两个等腰直角三角形（△ABC，△ADE），如图1所示放置，使得一直角边重合，连接BD，CE．
（1）说明BD=CE；
（2）延长BD，交CE于点F，求∠BFC的度数；
（3）若如图2放置，上面的结论还成立吗？请简单说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】“端午节”是我国的传统佳节，民间历来有吃“粽子”的习俗．我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽（以下分别用A，B，C，D表示）这四种不同口味粽子的喜爱情况，在节前对某居民区市民进行了抽样调查，并将调查情况绘制成如下两幅统计图（尚不完整）．
请根据以上信息回答：
（1）将两幅不完整的图补充完整；
（2）本次参加抽样调查的居民有多少人？
（3）若居民区有8000人，请估计爱吃D粽的人数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】完成下面的解题过程（在下面的横线上，填写相应的结论或推理的依据）：
已知：△ABC，∠A、∠B、∠C之和为多少？为什么？
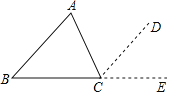
解：∠A+∠B+∠C=180°
理由：过C作CD//AB，并延长BC到E
∵CD//________（已作）
∴∠________=∠ACD（两直线平行，内错角相等）
且∠B=∠___________（________________）
而∠DCE+∠ACD+∠ACB=_________°
∴∠________+∠B+∠ACB=180°（__________）
-
科目： 来源： 题型：
查看答案和解析>>【题目】某学校为了庆祝校园艺术节,准备购买一批盆花布置校园.已知1盆A种花和2盆B种花一共需13元,2盆A种花和1盆B种花一共需11元.
(1)求1盆A种花和1盒B种花的售价各是多少元?
(2)学校准备购进这两种盆花共100盆,并且A种盆花的数量不超过B种盆花数量的2倍,请求出A种盆花的数量最多是多少?
相关试题
