【题目】如图,在直角梯形ABCD中,AB//CD,AD⊥AB,∠B=60°,AB=10,BC=4,点P沿线段AB从点A向点B运动,设AP=x,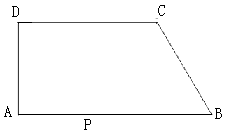
(1)求AD的长;
(2)点P在运动过程中,是否存在以A、P、D为顶点的三角形与以P、C、B为顶点的三角形相似?若存在,求出x的值;若不存在,请说明理由;
(3)直接写出:当△CDP为等腰三角形时x的值.
参考答案:
【答案】
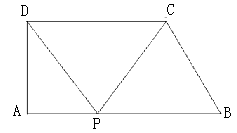
(1)解:过点D作DE//BC交AB于点E,
∵BE//CD,DE//BC,
∴四边形BCDE是平行四边形,
又∵BC=4,
∴DE=BC=4,
∵DE//BC,∠B=60°,
∴∠DEA=∠B=60°,
∵AD⊥AB,
∴∠A=90°,
∴∠ADE= 90°-∠DEA=30°,
∴AE=![]() DE=2,
DE=2,
∴AD=![]() =2
=2![]() .
.
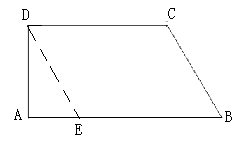
(2)解:∵△ADP中,∠A=90°,
∴△PBC是直角三角形,
∵∠B=60°,
∴∠BPC=90°或∠BCP=90°,
①当∠BPC=90°时,△BCP≌△EDA,
∴AE=BP=2,CP=AD=2![]() ,
,
∴AP=x=AB-BP=10-2=8,
∴![]() ≠
≠![]() ,
,
又∵∠A=∠BPC=90°,
∴△ADP与△CPB不相似;
②当∠BCP=90°时,∠BPC=90°-∠B=30°,
∵BC=4,AB=10,
∴BP=2BC=8,AP=x=AB-BP=10-8=2,
∴![]() =
=![]() =2,
=2,
又∵∠A=∠BCP=90°,
∴△ADP∽△CPB,
综上可知,x=2时,结论成立.
(3)解:①当PD=PC时,x=4;
②DP=DC时, x= 2![]() ;
;
③PC=CD时,x=8-2![]() .
.
【解析】解:(3)作CF⊥AB交AB于F,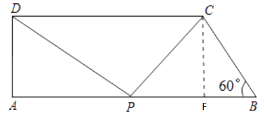
∵BC=4,∠B=60°,
∴BF=![]() BC=2,
BC=2,
∵AB=10,
∴AF=CD=10-2=8,
∵AP=x,AD=2![]() ,
,
∴PF=8-x,CF=2![]() ,
,
①当PD=PC时,
∴AD2+AP2=PF2+CF2,
即x2=(8-x)2,
∴x=4;
②DP=DC=8时,
∴AD2+AP2=DP2,
即12+x2=64,
∴x= 2![]() ;
;
③PC=CD=8时,
∴PF2+CF2=PC2,
即12+(8-x)2=64,
∴x=8-2![]() .
.
【考点精析】本题主要考查了勾股定理的概念和平行四边形的判定与性质的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,点A(1,0)、B(3,1)、C(3,3);反比例函数
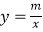 (x>0)的图象经过点D,点P是一次函数 y=kx+33k (k≠0)的图象与该反比例函数图象的一个公共点.
(x>0)的图象经过点D,点P是一次函数 y=kx+33k (k≠0)的图象与该反比例函数图象的一个公共点.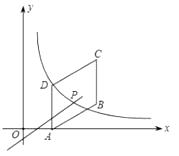
(1)求反比例函数的关系式;
(2)通过计算:说明一次函数 y=kx+33k 的图象一定经过点C;
(3)当一次函数 y=kx+33k 的图象平分平行四边形ABCD的面积时,求此一次函数的关系式。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AM、CM平分∠BAD和∠BCD,若∠B=34°,∠D=42°,则∠M=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】a﹣p=
 (a≠0),即a的负P次幂等于a的p次幂的倒数.例:4﹣2=
(a≠0),即a的负P次幂等于a的p次幂的倒数.例:4﹣2=
(1)计算:5﹣2= ;(﹣2)﹣2= ;
(2)如果2﹣p=
 ,那么p= ;如果a﹣2=
,那么p= ;如果a﹣2= ,那么a= ;
,那么a= ;(3)如果a﹣p=
 ,且a、p为整数,求满足条件的a、p的取值.
,且a、p为整数,求满足条件的a、p的取值. -
科目: 来源: 题型:
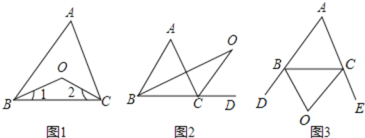
查看答案和解析>>【题目】认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.
(1)如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,试证明∠BOC=90°+
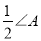
(2)如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
(3)如图3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(只写结论,不需证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,定点E,F分别在直线AB,CD上,平行线AB,CD之间有一动点P.
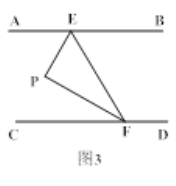
(1)如图1,当P点在EF的左侧时,∠AEP,∠EPF,∠PFC满足数量关系为 ,如图2,当P点在EF的右侧时,∠AEP,∠EPF,∠PFC满足数量关系为 .
(2)如图3,当∠EPF=90°,FP平分∠EFC时,求证:EP平分∠AEF;
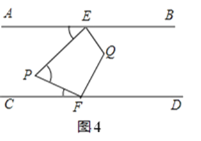
(3)如图4,QE,QF分别平分∠PEB和∠PFD,且点P在EF左侧.
①若∠EPF=60°,则∠EQF= .
②猜想∠EPF与∠EQF的数量关系,并说明理由;
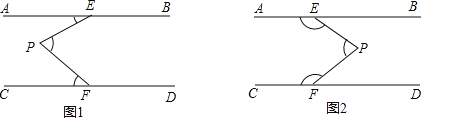
-
科目: 来源: 题型:
查看答案和解析>>【题目】顺次连结矩形四边中点所得的四边形一定是( )
A.菱形
B.矩形
C.正方形
D.等腰梯形
相关试题

