【题目】如图,AB∥CD,定点E,F分别在直线AB,CD上,平行线AB,CD之间有一动点P.
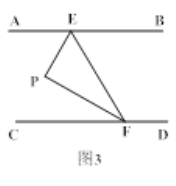
(1)如图1,当P点在EF的左侧时,∠AEP,∠EPF,∠PFC满足数量关系为 ,如图2,当P点在EF的右侧时,∠AEP,∠EPF,∠PFC满足数量关系为 .
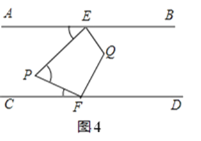
(2)如图3,当∠EPF=90°,FP平分∠EFC时,求证:EP平分∠AEF;
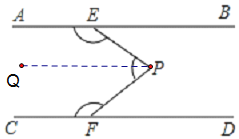
(3)如图4,QE,QF分别平分∠PEB和∠PFD,且点P在EF左侧.
①若∠EPF=60°,则∠EQF= .
②猜想∠EPF与∠EQF的数量关系,并说明理由;
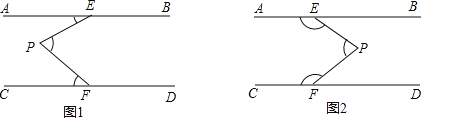
参考答案:
【答案】(1)∠EPF=∠AEP+∠PFC,∠AEP+∠EPF+∠PFC=360°;(2)见解析;(3)①150°,∠EQF=180°-![]() ∠EPF
∠EPF
【解析】
(1)如下图,过点P作AB的平行线,根据平行线的性质可推导出角度关系;
(2)如下图,根据(1)的结论,可得∠AEP+∠PFC=∠EPF=90°,利用△EPF内角和为180°可推导得出∠PEF+∠PFE=90°,从而得出∠PEF=∠AEP;
(3)①根据(1)的结论知:∠AEP+∠PFC=∠EPF=60°,再利用角平分线的性质得出∠PEQ+∠PFQ=150°,最后在四边形EPFQ中得出结论;
②根据(1)的结论知:∠AEP+∠PFC=∠EPF°,再利用角平分线的性质得出∠PEQ+∠PFQ=180°-![]() ,最后在四边形EPFQ中得出结论.
,最后在四边形EPFQ中得出结论.
(1)如下图,过点P作PQ∥AB

∵PQ∥AB,AB∥CD,∴PQ∥CD
∴∠AEP=∠EPQ,∠QPF=∠PFC
又∵∠EPF=∠EPQ+∠QPF
∴∠EPF=∠AEP+∠PFC
如下图,过点P作PQ∥AB
同理,AB∥QP∥CD
∴∠AEP+∠QPE=180°,∠QPF+∠PFC=180°
∴∠AEP+∠EPF+∠PFC=∠AEP+∠EPQ+∠QPF+∠PFC=360°
(2)根据(1)的结论知:∠AEP+∠PFC=∠EPF=90°
∵PF是∠CFE的角平分线,∴∠PFC=∠PFE
在△PEF中,∵∠EPF=90°,∴∠PEF+∠PFE=90°
∴∠PEF+∠PFE=∠AEP+∠PFC
∴∠PEF=∠AEP,∴PE是∠AEF的角平分线
(3)①根据(1)的结论知:∠AEP+∠PFC=∠EPF=60°
∴∠BEP+∠PFD=180°-∠AEP+180°-∠PFC=300°
∵EQ、QF分别是∠PEB和∠PFD的角平分线
∴∠PEQ=QEB,∠PFQ=∠QFD
∴∠PEQ+∠PFQ=150°
在四边形PEQF中,∠EQF=360°-∠EPF-(∠PEQ+∠PFQ)=360°-60°-150°=150°
②根据(1)的结论知:∠AEP+∠PFC=∠EPF
∴∠BEP+∠PFD=180°-∠AEP+180°-∠PFC=360°-∠EPF
∵EQ、QF分别是∠PEB和∠PFD的角平分线
∴∠PEQ=∠QEB,∠PFQ=∠QFD
∴∠PEQ+∠PFQ=![]() =180°-
=180°-![]()
∴在四边形PEQF中:
∠EQF=360°-∠EPF-(∠PEQ+∠PFQ)=360°-![]() -(180°-
-(180°-![]() )=180°-
)=180°-![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】a﹣p=
 (a≠0),即a的负P次幂等于a的p次幂的倒数.例:4﹣2=
(a≠0),即a的负P次幂等于a的p次幂的倒数.例:4﹣2=
(1)计算:5﹣2= ;(﹣2)﹣2= ;
(2)如果2﹣p=
 ,那么p= ;如果a﹣2=
,那么p= ;如果a﹣2= ,那么a= ;
,那么a= ;(3)如果a﹣p=
 ,且a、p为整数,求满足条件的a、p的取值.
,且a、p为整数,求满足条件的a、p的取值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形ABCD中,AB//CD,AD⊥AB,∠B=60°,AB=10,BC=4,点P沿线段AB从点A向点B运动,设AP=x,
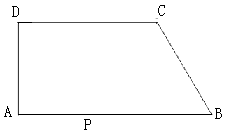
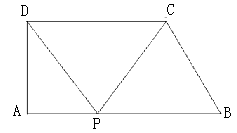
(1)求AD的长;
(2)点P在运动过程中,是否存在以A、P、D为顶点的三角形与以P、C、B为顶点的三角形相似?若存在,求出x的值;若不存在,请说明理由;
(3)直接写出:当△CDP为等腰三角形时x的值. -
科目: 来源: 题型:
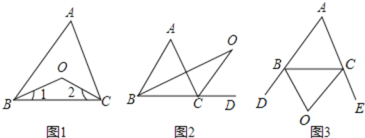
查看答案和解析>>【题目】认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.
(1)如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,试证明∠BOC=90°+
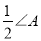
(2)如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
(3)如图3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(只写结论,不需证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】顺次连结矩形四边中点所得的四边形一定是( )
A.菱形
B.矩形
C.正方形
D.等腰梯形 -
科目: 来源: 题型:
查看答案和解析>>【题目】在下列条件中:①∠A+∠B=∠C,②∠A∶∠B∶∠C=1∶5∶6,③∠A=90°-∠B,④∠A=∠B=
 ∠C中,能确定△ABC是直角三角形的条件有 ( )
∠C中,能确定△ABC是直角三角形的条件有 ( )A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别是AE=1,CF=2,则EF长为 .

相关试题

