【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上运动(
上运动(![]() 不与
不与![]() 、
、![]() 重合),连接
重合),连接![]() ,作
,作![]() ,
,![]() 交线段
交线段![]() 于
于![]() .
.


(1)当![]() 时,
时,![]() = ,
= ,![]() = ;点
= ;点![]() 从
从![]() 向
向![]() 运动时,
运动时,![]() 逐渐 (填“增大”或“减小”);
逐渐 (填“增大”或“减小”);
(2)当![]() 等于多少时,
等于多少时,![]() ,请说明理由;
,请说明理由;
(3)在点![]() 的运动过程中,
的运动过程中,![]() 的形状可以是等腰三角形吗?若可以,请直接写出
的形状可以是等腰三角形吗?若可以,请直接写出![]() 的度数.若不可以,请说明理由.
的度数.若不可以,请说明理由.
参考答案:
【答案】(1)40°,100°;减小;(2)当DC=2时,△ABD≌△DCE;理由见解析;(3)当∠ADB=110°或80°时,△ADE是等腰三角形.
【解析】
(1)利用平角的定义可求得∠EDC的度数,再根据三角形内角定理即可求得∠DEC的度数,利用三角形外角的性质可判断∠BDA的变化情况;
(2)利用∠ADC=∠B+∠BAD,∠ADC=∠ADE+∠EDC得出∠BAD=∠EDC,进而求出△ABD≌△DCE;
(3)根据等腰三角形的判定以及分类讨论得出即可.
(1)∵∠BDA=100°,∠ADE=40°,∠BDA+∠ADE+∠EDC=180°,
∴∠EDC=180°-100°-40°=40°,
∵∠EDC+∠DEC+∠C=180°,∠C=40°,
∴∠DEC=180°-40°-40°=100°;
∵∠BDA=∠C+∠DAC,∠C=40°,
点D从B向C运动时,∠DAC逐渐减小,
∴点D从B向C运动时,∠BDA逐渐减小,
故答案为:40°,100°;减小;
(2)当DC=2时,△ABD≌△DCE;
理由:∵∠ADE=40°,∠B=40°,
又∵∠ADC=∠B+∠BAD,∠ADC=∠ADE+∠EDC.
∴∠BAD=∠EDC.
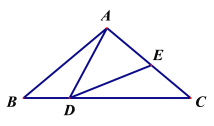
在△ABD和△DCE中,
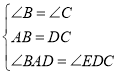 ,
,
∴△ABD≌△DCE(ASA);
(3)①当AD=AE时,∠ADE=∠AED=40°,
∵∠AED>∠C,
∴此时不符合;
②当DA=DE时,即∠DAE=∠DEA=![]() (180°-40°)=70°,
(180°-40°)=70°,
∵∠BAC=180°-40°-40°=100°,
∴∠BAD=100°-70°=30°;
∴∠BDA=180°-30°-40°=110°;
③当EA=ED时,∠ADE=∠DAE=40°,
∴∠BAD=100°-40°=60°,
∴∠BDA=180°-60°-40°=80°;
∴当∠ADB=110°或80°时,△ADE是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC为等边三角形,点E、F分别在BC和AB上,且CE=BF,AE与CF相交于点H.
(1)求证:△ACE≌△CBF;
(2)求∠CHE的度数;
(3)如图2,在图1上以AC为边长再作等边△ACD,将HE延长至G使得HG=CH,连接HD与CG,求证:HD=AH+CH

-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是中国电信两种“
 套餐”计费方式.(月基本费固定收,主叫不超过主叫时间,流量不超上网流量不再收取额外费用费,主叫超时和上网超流量部分加收超时费和超流量费)
套餐”计费方式.(月基本费固定收,主叫不超过主叫时间,流量不超上网流量不再收取额外费用费,主叫超时和上网超流量部分加收超时费和超流量费)月基本费/元
主叫通话/分钟
上网流量/MB
接听
主叫超时(元/分钟)
超出流量(元/MB)
套餐1
49
200
500
免费
0.20
0.3
套餐2
69
250
600
免费
0.15
0.2
(1)6月小王主叫通话时间220分钟,上网流量800MB.按套餐1计费需 元,按套餐2计费需 元;
若他按套餐2计费需129元,主叫通话时间为240分钟,则他上网使用了 MB流量;
(2)若上网流量为540MB,是否存在某主叫通话时间
 (分钟),按套餐1和套餐2的计费相等?若存在,请求出
(分钟),按套餐1和套餐2的计费相等?若存在,请求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在图1中,已知∠MAN=120°,AC平分∠MAN.∠ABC=∠ADC=90°,则能得如下两个结论:① DC = BC; ②AD+AB=AC.请你证明结论②;
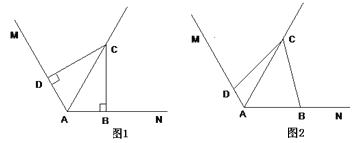
(2)在图2中,把(1)中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°,其他条件不变,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°. 若坡角∠FAE=30°,求大树的高度. (结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,
 ≈1.73)
≈1.73)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)12-(-18)+(-7)-15
(2)(-2.7)+(+1
 )-(-6.7)+(-1.6)
)-(-6.7)+(-1.6)(3)20+(-14)-(-18)-13
(4)81÷|-2
 |×
|×
(5)

(6)-14-(1-0.5×
 )×(2-23)
)×(2-23) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三个边长均为4的正方形重叠在一起,O1,O2是其中左侧两个正方形的对角线交点,同时O1,O2也是右侧两个正方形的顶点,根据教材第63页《实践与探究》活动中有关内容,可知阴影部分面积是( )

A.2B.4C.6D.8
相关试题

