【题目】下表是中国电信两种“![]() 套餐”计费方式.(月基本费固定收,主叫不超过主叫时间,流量不超上网流量不再收取额外费用费,主叫超时和上网超流量部分加收超时费和超流量费)
套餐”计费方式.(月基本费固定收,主叫不超过主叫时间,流量不超上网流量不再收取额外费用费,主叫超时和上网超流量部分加收超时费和超流量费)
月基本费/元 | 主叫通话/分钟 | 上网流量/MB | 接听 | 主叫超时(元/分钟) | 超出流量(元/MB) | |
套餐1 | 49 | 200 | 500 | 免费 | 0.20 | 0.3 |
套餐2 | 69 | 250 | 600 | 免费 | 0.15 | 0.2 |
(1)6月小王主叫通话时间220分钟,上网流量800MB.按套餐1计费需 元,按套餐2计费需 元;
若他按套餐2计费需129元,主叫通话时间为240分钟,则他上网使用了 MB流量;
(2)若上网流量为540MB,是否存在某主叫通话时间![]() (分钟),按套餐1和套餐2的计费相等?若存在,请求出
(分钟),按套餐1和套餐2的计费相等?若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
参考答案:
【答案】(1)143;109;900;(2)t=240.
【解析】
(1)分别根据套餐1、2中主叫超时的收费标准以及超出流量的收费标准进行计算可得具体的费用;按套餐2计费需129元,根据套餐2的标准求出超出的流量部分即可求得上网使用的总流量;
(2)分主叫时间不超过200分钟、超过200分钟而不超过250分钟、超过250分钟三种情况分别根据套餐1、2的标准可得关于t的式子,再根据按套餐1和套餐2的计费相等可得关于t的方程,解方程即可得.
(1)主叫通话时间220分钟,上网流量800MB时,
套餐1:主叫超时话费:0.20×(220-200)=4(元),
超出流量的费用:0.3×(800-500)=90(元)
套餐1需:49+4+90=143(元);
套餐2:220<250,主叫不超时,
超出流量的费用:0.2×(800-600)=40(元)
套餐2需:69+40=109(元);
若按套餐2计费需129元,240<250,此时主叫不超时,
超出上网流量为:(129-69)÷0.2=300(MB),
上网使用了600+300=900MB,
故答案为:143;109;900;
(2)存在,t=240,理由如下:
若主叫时间t不超过200分钟,
按套餐1计费为:49+0.3×(540-500)=49+12=61<69,此时套餐1与套餐2计费不相等;
若主叫时间t超过200分钟而不超过250分钟,
按套餐1计费为:49+0.3×(540-500)+0.2(t-200)=0.2t+21,
按套餐2计费为:69,
若套餐1、套餐2计费相等,则有0.2t+21=69,解得:t=240;
若主叫时间t超过250分钟,
按套餐1计费为:49+0.3×(540-500)+0.2(t-200)=0.2t+21,
按套餐2计费为:69+0.15(t-250)=0.15t+31.5,
若套餐1、套餐2计费相等,则有0.2t+21=0.15t+31.5,解得t=210(不符题意,舍去),
综上,当主叫时间为240分钟时,套餐1和套餐2的计费相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
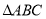 中,
中, 、
、 分别垂直平分
分别垂直平分 和
和 ,交
,交 于
于 、
、 两点,
两点, 与
与 相交于点
相交于点 .
.
(1)若
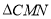 的周长为15 cm,求
的周长为15 cm,求 的长.
的长.(2)若
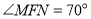 ,求
,求 的度数.
的度数. -
科目: 来源: 题型:
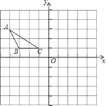
查看答案和解析>>【题目】已知:如图,在△ABC中,点A的坐标为(﹣4,3),点B的坐标为(﹣3,1),BC=2,BC∥x轴.
(1)画出△ABC关于y轴对称的图形△A1B1C1;并写出A1,B1,C1的坐标;
(2)求以点A、B、B1、A1为顶点的四边形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC为等边三角形,点E、F分别在BC和AB上,且CE=BF,AE与CF相交于点H.
(1)求证:△ACE≌△CBF;
(2)求∠CHE的度数;
(3)如图2,在图1上以AC为边长再作等边△ACD,将HE延长至G使得HG=CH,连接HD与CG,求证:HD=AH+CH

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在图1中,已知∠MAN=120°,AC平分∠MAN.∠ABC=∠ADC=90°,则能得如下两个结论:① DC = BC; ②AD+AB=AC.请你证明结论②;
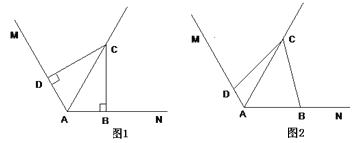
(2)在图2中,把(1)中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°,其他条件不变,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,点
,点 在线段
在线段 上运动(
上运动( 不与
不与 、
、 重合),连接
重合),连接 ,作
,作 ,
, 交线段
交线段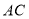 于
于 .
.

(1)当
 时,
时, = ,
= , = ;点
= ;点 从
从 向
向 运动时,
运动时, 逐渐 (填“增大”或“减小”);
逐渐 (填“增大”或“减小”);(2)当
 等于多少时,
等于多少时, ,请说明理由;
,请说明理由;(3)在点
 的运动过程中,
的运动过程中, 的形状可以是等腰三角形吗?若可以,请直接写出
的形状可以是等腰三角形吗?若可以,请直接写出 的度数.若不可以,请说明理由.
的度数.若不可以,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°. 若坡角∠FAE=30°,求大树的高度. (结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,
 ≈1.73)
≈1.73)
相关试题

