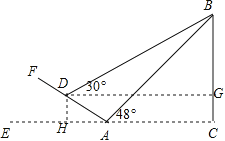
【题目】如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°. 若坡角∠FAE=30°,求大树的高度. (结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11, ![]() ≈1.73)
≈1.73)

参考答案:
【答案】13米.
【解析】试题分析:根据矩形性质得出DG=CH,CG=DH,再利用锐角三角函数的性质求出问题即可.
试题解析:如图,过点D作DG⊥BC于GDH⊥CE于H,
则四边形DHCG为矩形.
故DG=CH,CG=DH,
在直角三角形AHD中,
∵∠DAH=30°,AD=6,
∴DH=3,AH=3![]() ,
,
∴CG=3,
设BC为x,
在直角三角形ABC中,AC=![]() ,
,
∴DG=3![]() +
+![]() ,BG=x-3,
,BG=x-3,
在直角三角形BDG中,∵BG=DGtan30°,
∴x-3=(3![]() +
+![]() )
)![]()
解得:x≈13,
∴大树的高度为:13米.
-
科目: 来源: 题型:
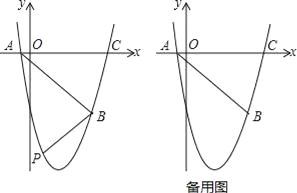
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)经过点 经过点A(﹣1,0),B(5,﹣6),C(6,0)
(1)求抛物线的解析式;
(2)如图,在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点Q为抛物线的对称轴上的一个动点,试指出△QAB为等腰三角形的点Q一共有几个?并请求出其中某一个点Q的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知七名选手参加演讲比赛,所得分数各不同.其中一名选手想知道自己能否进入前四名,他除了知道他本人的分数外,还要知道七名选手分数的( )
A. 中位数B. 众数C. 平均数D. 方差
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题:
(1)甲乙两地之间的距离为______千米;
(2)求快车和慢车的速度;
(3)求线段DE所表示的y与x之间的函数关系式,并写出自变量x的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是矩形ABCD的边AD上的一个动点,矩形的两条边AB、BC的长分别为3和4,那么点P到矩形的两条对角线AC和BD的距离之和是( )

A.
B.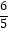
C.
D.不确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】近似数4.50所表示的准确值a的取值范围是( )
A.4.495≤a<4.505
B.4040≤a<4.60
C.4.495≤a≤4.505
D.4.500≤a<4.5056 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中计算正确的是( )
A. 2x+3y=5xyB. x2x3=x5
C. (a+b)2=a2+b2D. (3a3)2=9a5
相关试题

