【题目】如图,三个边长均为4的正方形重叠在一起,O1,O2是其中左侧两个正方形的对角线交点,同时O1,O2也是右侧两个正方形的顶点,根据教材第63页《实践与探究》活动中有关内容,可知阴影部分面积是( )

A.2B.4C.6D.8
参考答案:
【答案】D
【解析】
标注字母,作正方形两邻边的垂线![]() ,根据正方形的中心到各边的距离相等可得
,根据正方形的中心到各边的距离相等可得![]() ,根据同角的余角相等求出∠1=∠2,再利用“角边角”△
,根据同角的余角相等求出∠1=∠2,再利用“角边角”△![]() ≌△
≌△![]() ,再根据全等三角形的面积相等求出阴影部分的面积等于正方形的面积的
,再根据全等三角形的面积相等求出阴影部分的面积等于正方形的面积的![]() ,同理可得另一阴影部分的面积也等于正方形面积的
,同理可得另一阴影部分的面积也等于正方形面积的![]() ,最后根据正方形的面积公式列式进行计算即可得解.
,最后根据正方形的面积公式列式进行计算即可得解.
解:如图,作正方形两邻边的垂线![]() ,
,
∵![]() 是正方形的中心, ∴
是正方形的中心, ∴![]() ,
,
∵∠1+![]() ∠2+
∠2+![]()
∴∠1=∠2,
∵在△![]() 和△
和△![]() 中,
中,
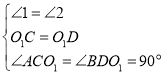
∴△![]() ≌△
≌△![]() ,
,
∴阴影部分的面积= ![]() S正方形,
S正方形,
同理可得:另一阴影部分的面积=![]() S正方形,
S正方形,
∵正方形的边长为![]() cm,
cm,
∴阴影部分的面积=![]() ×
×![]()
故选:.D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
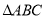 中,
中, ,
, ,点
,点 在线段
在线段 上运动(
上运动( 不与
不与 、
、 重合),连接
重合),连接 ,作
,作 ,
, 交线段
交线段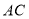 于
于 .
.

(1)当
 时,
时, = ,
= , = ;点
= ;点 从
从 向
向 运动时,
运动时, 逐渐 (填“增大”或“减小”);
逐渐 (填“增大”或“减小”);(2)当
 等于多少时,
等于多少时, ,请说明理由;
,请说明理由;(3)在点
 的运动过程中,
的运动过程中, 的形状可以是等腰三角形吗?若可以,请直接写出
的形状可以是等腰三角形吗?若可以,请直接写出 的度数.若不可以,请说明理由.
的度数.若不可以,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°. 若坡角∠FAE=30°,求大树的高度. (结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,
 ≈1.73)
≈1.73)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)12-(-18)+(-7)-15
(2)(-2.7)+(+1
 )-(-6.7)+(-1.6)
)-(-6.7)+(-1.6)(3)20+(-14)-(-18)-13
(4)81÷|-2
 |×
|×
(5)

(6)-14-(1-0.5×
 )×(2-23)
)×(2-23) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ABC=90°,点D,F分别是AC,AB的中点,CE∥DB,BE∥DC.
(1)求证:四边形DBEC是菱形;
(2)若AD=3,DF=1,求四边形DBEC面积.
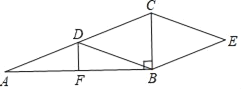
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,四边形ABCD是正方形,M是AB延长线上一点.直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A、B重合),另一直角边与∠CBM的平分线BF相交于点F.

(1)如图1,当点E在AB边得中点位置时:
①通过测量DE、EF的长度,猜想DE与EF满足的数量关系是 .
②连接点E与AD边的中点N,猜想NE与BF满足的数量关系是 ,请证明你的猜想.
(2)如图2,当点E在AB边上的任意位置时,猜想此时DE与EF有怎样的数量关系,并证明你的猜想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一自行车厂计划一周生产自行车1400辆,平均每天生产200辆,但由于种种原因,实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产记为正,减产记为负

(1)根据记录的数据可知该厂星期四生产自行车多少辆?
(2)根据记录的数据可知该厂本周实际生产自行车多少辆?
(3)产量最多的一天比产量最少的一天多生产自行车多少辆?
(4)该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超出部分每辆另加15元,少生产一辆扣20元,那么该厂工人这一周的工资总额是多少?
相关试题

