【题目】已知a是最大的负整数,b、c满足![]() ,且a,b,c分别是点A,B,C在数轴上对应的数.
,且a,b,c分别是点A,B,C在数轴上对应的数.
(1)求a,b,c的值,并在数轴上标出点A,B,C;
![]()
(2)若动点P从C出发沿数轴正方向运动,点P的速度是每秒2个单位长度,运动几秒后,点P到达B点?
(3)在数轴上找一点M,使点M到A,B,C三点的距离之和等于13,请直接写出所有点M对应的数.(不必说明理由)
参考答案:
【答案】(1)a=-1,b=3,c=-4.数轴见解析;(2)![]() 秒.(3)
秒.(3)![]() 或-5.
或-5.
【解析】
(1)根据绝对值和偶次幂具有非负性可得b-3=0,c+4=0,进而可得答案;
(2)根据(1)中的数据得到BC=7,结合运动时间=运动路程÷运动速度解答;
(3)注意数轴上两点间的距离公式:两点所对应的数的差的绝对值.
(1)∵a是最大的负整数,
∴a=-1,
∵|b-3|+(c+4)2=0,
∴b-3=0,c+4=0,
∴b=3,c=-4.
表示在数轴上为:
![]()
(2)BC=3-(-4)=7,则运动时间为![]() 秒.
秒.
(3)设点M表示的数为x,使P到A、B、C的距离和等于13,
①当M在点B的右侧,x-(-4)+x-(-1)+x-3=13.
解得x=![]() ,
,
即M对应的数是![]() .
.
②当M在C点左侧,(-4)-x+(-1)-x+3-x=13.
解得x=-5,
即M对应的数是-5.
综上所述,点M表示的数是![]() 或-5.
或-5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)3x+7=32-2x
(2)

(3)
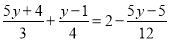
(4)x的5倍与2的和等于x的3倍与4的差,求x;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,BAC 90o,D是BC的中点,E是AD的中点,过点A作AF//BC 交 BE的延长线于点F,连接CF.
(1)求证:AD=AF.
(2)当AB=AC=
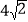 时,求四边形ADCF 的面积.
时,求四边形ADCF 的面积.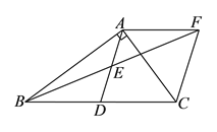
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角
 中,
中, ,
,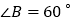 ,AD,CE分别是
,AD,CE分别是 和
和 的平分线,AD,CE相交于点F.
的平分线,AD,CE相交于点F. 求
求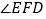 的度数;
的度数; 判断FE与FD之间的数量关系,并证明你的结论.
判断FE与FD之间的数量关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以 Rt△ ABC 的直角边 AC 及斜边 AB 向外作等边△ ACD,等边△ ABE.已知∠ABC=60°,EF⊥AB,垂足为 F,连接 DF.
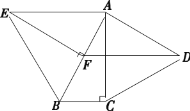
(1)证明:△ACB≌△EFB;
(2)求证:四边形 ADFE 是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明家买了一辆小轿车,小明连续记录了一周每天行驶的路程:

请你用学过的统计知识解决下面的问题:
(1)小明家的轿车每月(按30天计算)要行驶多少千米?
(2)若每行驶100千米需汽油8升,汽油每升6.64元,请你算出小明家一年(按12个月计算)的汽油费用大约是多少元(精确到百位).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数与反比例函数的图像交于A(1,12)和B(6,2)两点。点P是线段AB上一动点(不与点A和B重合),过P点分别作x、y轴的垂线PC、PD交反比例函数图像于点M、N,则四边形PMON面积的最大值是( )
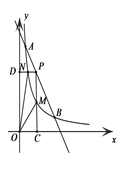
A.
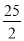 B.
B.  C. 6 D. 12
C. 6 D. 12
相关试题

