【题目】在直角![]() 中,
中,![]() ,
,![]() ,AD,CE分别是
,AD,CE分别是![]() 和
和![]() 的平分线,AD,CE相交于点F.
的平分线,AD,CE相交于点F.
![]() 求
求![]() 的度数;
的度数;
![]() 判断FE与FD之间的数量关系,并证明你的结论.
判断FE与FD之间的数量关系,并证明你的结论.

参考答案:
【答案】(1)120°;(2)见解析.
【解析】
(1)由已知条件易得∠BAC=30°,结合AD,CE分别是∠BAC和∠ACB的角平分线可得∠FAC=15°,∠FCA=45°,由此结合三角形内角和定理可得∠AFC=120°,由此即可得到∠EFD=∠AFC=120°.
(2)如下图,在AC是截取AG=AE,连接FG,在由已知条件易证△AGF≌△AEF,由此可得∠AFG=∠AFE=∠FAC+∠ECA=60°,结合∠AFC=120°,可得∠CFG=60°,∠CFD=60°,这样结合∠GCF=∠DCF,CF=CF即可得到△GCF≌△DCF,由此可得FG=FD,结合FE=FG即可得到FE=FD.
(1)∵![]() 中,
中,![]() ,
,![]()
∴![]() ,
,
∵![]() 、CE分别是
、CE分别是![]() 、
、![]() 的平分线,
的平分线,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;
![]() 与FD之间的数量关系为
与FD之间的数量关系为![]() ;
;
在AC上截取![]() ,连接FG,
,连接FG,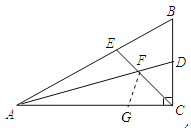
∵![]() 是
是![]() 的平分线,
的平分线,
∴![]()
在![]() 和
和![]() 中,∵
中,∵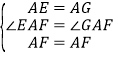 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,∠AFG=∠AFE=∠FAC+∠ECA=60°,
,∠AFG=∠AFE=∠FAC+∠ECA=60°,
∴∠CFD=∠AFE=60°,
∴∠CFD=∠CFG,
∵在![]() 和
和![]() 中,
中,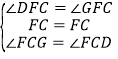 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点B出发,沿对角线BD向点D匀速运动,速度为4cm/s,过点P作PQ⊥BD交BC于点Q,以PQ为一边作正方形PQMN,使得点N落在射线PD上,点O从点D出发,沿DC向点C匀速运动,速度为3m/s,以O为圆心,0.8cm为半径作⊙O,点P与点O同时出发,设它们的运动时间为t(单位:s)(0<t<
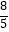 ).
). 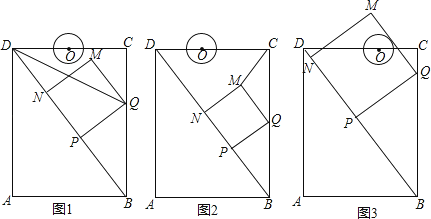
(1)如图1,连接DQ平分∠BDC时,t的值为;
(2)如图2,连接CM,若△CMQ是以CQ为底的等腰三角形,求t的值;
(3)请你继续进行探究,并解答下列问题:
①证明:在运动过程中,点O始终在QM所在直线的左侧;
②如图3,在运动过程中,当QM与⊙O相切时,求t的值;并判断此时PM与⊙O是否也相切?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l:y=﹣3x+3与x轴、y轴分别相交于A、B两点,抛物线y=ax2﹣2ax+a+4(a<0)经过点B.

(1)求该抛物线的函数表达式;
(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,设点M的横坐标为m,△ABM的面积为S,求S与m的函数表达式,并求出S的最大值;
(3)在(2)的条件下,当S取得最大值时,动点M相应的位置记为点M′.
①写出点M′的坐标;
②将直线l绕点A按顺时针方向旋转得到直线l′,当直线l′与直线AM′重合时停止旋转,在旋转过程中,直线l′与线段BM′交于点C,设点B、M′到直线l′的距离分别为d1、d2 , 当d1+d2最大时,求直线l′旋转的角度(即∠BAC的度数). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,
, ,BE与CF交于点D,则对于下列结论:
,BE与CF交于点D,则对于下列结论: ≌
≌ ;
; ≌
≌ ;
; ≌
≌ ;
; 在
在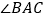 的平分线上
的平分线上 其中正确的是( )
其中正确的是( )
A. ①②③ B. ②③④ C. ①③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】同学们都知道,|2-(-1)|表示2与-1的差的绝对值,实际上位可理解为在数轴上正数2对应的点与负数一1对应的点之间的距离,试探索:
(1)|2-(-1)|=______;如果|x-1|=2,则x=______.
(2)求|x-2|+|x-4|的最小值,并求此时x的取值范围;
(3)由以上探素已知(|x-2|+|x+4|)(|y-1|+|y-6|)=10,求x+y的最大值与最小值;
(4)由以上探索及猜想,计算|x-1|+|x-2|+|x-3|+…+|x-2017|+|x-2018|的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】试比较下列两个方程的异同,
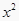 +2x-3=0,
+2x-3=0,  +2x+3=0.
+2x+3=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b、c为三角形三个边,
 +bx(x-1)=
+bx(x-1)=  -2b是关于x的一元二次方程吗?
-2b是关于x的一元二次方程吗?
相关试题

