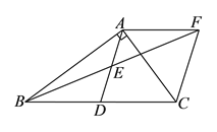
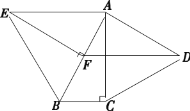
【题目】如图,在Rt△ABC中,BAC 90o,D是BC的中点,E是AD的中点,过点A作AF//BC 交 BE的延长线于点F,连接CF.
(1)求证:AD=AF.
(2)当AB=AC=![]() 时,求四边形ADCF 的面积.
时,求四边形ADCF 的面积.
参考答案:
【答案】(1)证明见解析(2)16
【解析】分析:(1)E是AD的中点,AF∥BC,,易证得△AEF≌△DEB,即可得AF=BD,又由在△ABC中,∠BAC=90°,AD是中线,根据直角三角形斜边的中线等于斜边的一半,即可证得![]() 即可证得:
即可证得:![]() ;
;
![]() 证明四边形ADCF为正方形,根据正方形的面积公式进行计算即可.
证明四边形ADCF为正方形,根据正方形的面积公式进行计算即可.
详解:(1)证明:∵AF∥BC,
∴∠EAF=∠EDB,
∵E是AD的中点,
∴AE=DE,
在△AEF和△DEB中,
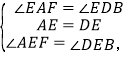
∴△AEF≌△DEB(ASA),
∴AF=BD,
∵在△ABC中,![]() ,AD是中线,
,AD是中线,
∴![]()
∴AD=AF;
(2)∵![]()
∴![]()
∵AF//BC,
∴四边形ADCF为平行四边形
∵![]() ,
,
∴平行四边形ADCF为菱形,
∵![]() ,
,
D是BC的中点,
∴四边形ADCF为正方形
∵ AB=AC=![]() ,
,
∴ BC=8,
∴ CD=4,
∴正方形ADCF的面积为16
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了提高科技创新意识,我市某中学在“2016年科技节”活动中举行科技比赛,包括“航模”、“机器人”、“环保”、“建模”四个类别(每个学生只能参加一个类别的比赛),各类别参赛人数统计如图:

请根据以上信息,解答下列问题:
(1)全体参赛的学生共有 人,“建模”在扇形统计图中的圆心角是 °;
(2)将条形统计图补充完整;
(3)在比赛结果中,获得“环保”类一等奖的学生为1名男生和2名女生,获得“建模”类一等奖的学生为1名男生和1名女生,现从这两类获得一等奖的学生中各随机选取1名学生参加市级“环保建模”考察活动,问选取的两人中恰为1男生1女生的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,
, ,BE与CF交于点D,则对于下列结论:
,BE与CF交于点D,则对于下列结论: ≌
≌ ;
; ≌
≌ ;
; ≌
≌ ;
; 在
在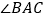 的平分线上
的平分线上 其中正确的是( )
其中正确的是( )
A. ①②③ B. ②③④ C. ①③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)3x+7=32-2x
(2)

(3)
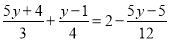
(4)x的5倍与2的和等于x的3倍与4的差,求x;
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角
 中,
中, ,
,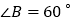 ,AD,CE分别是
,AD,CE分别是 和
和 的平分线,AD,CE相交于点F.
的平分线,AD,CE相交于点F. 求
求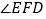 的度数;
的度数; 判断FE与FD之间的数量关系,并证明你的结论.
判断FE与FD之间的数量关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a是最大的负整数,b、c满足
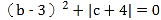 ,且a,b,c分别是点A,B,C在数轴上对应的数.
,且a,b,c分别是点A,B,C在数轴上对应的数.(1)求a,b,c的值,并在数轴上标出点A,B,C;
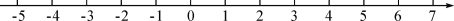
(2)若动点P从C出发沿数轴正方向运动,点P的速度是每秒2个单位长度,运动几秒后,点P到达B点?
(3)在数轴上找一点M,使点M到A,B,C三点的距离之和等于13,请直接写出所有点M对应的数.(不必说明理由)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以 Rt△ ABC 的直角边 AC 及斜边 AB 向外作等边△ ACD,等边△ ABE.已知∠ABC=60°,EF⊥AB,垂足为 F,连接 DF.
(1)证明:△ACB≌△EFB;
(2)求证:四边形 ADFE 是平行四边形.
相关试题

