【题目】如图,分别以 Rt△ ABC 的直角边 AC 及斜边 AB 向外作等边△ ACD,等边△ ABE.已知∠ABC=60°,EF⊥AB,垂足为 F,连接 DF.
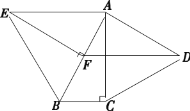
(1)证明:△ACB≌△EFB;
(2)求证:四边形 ADFE 是平行四边形.
参考答案:
【答案】(1)见详解;(2)见详解.
【解析】
(1)由△ABE是等边三角形可知:AB=BE,∠EBF=60°,于是可得到∠EFB=∠ACB=90°,∠EBF=∠ABC,接下来依据AAS证明△ABC≌△EBF即可;
(2)由△ABC≌△EBF可得到EF=AC,由△ACD是的等边三角形进而可证明AC=AD=EF,然后再证明∠BAD=90°,可证明EF∥AD,故此可得到四边形EFDA为平行四边形.
解:(1)证明:∵△ABE是等边三角形,EF⊥AB,
∴∠EBF=60°,AE=BE,∠EFB=90°.
又∵∠ACB=90°,∠ABC=60°,
∴∠EFB=∠ACB,∠EBF=∠ABC.
∵BE=BA,
∴△ABC≌△EBF(AAS).
(2)证明:∵△ABC≌△EBF,
∴EF=AC.
∵△ACD是的等边三角形,
∴AC=AD=EF,∠CAD=60°,
又∵Rt△ABC中,∠ABC=60°,∠BAC=30°,
∴∠BAD=∠BAC+∠CAD=90°,
∴∠EFA=∠BAD=90°,
∴EF∥AD.
又∵EF=AD,
∴四边形EFDA是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,BAC 90o,D是BC的中点,E是AD的中点,过点A作AF//BC 交 BE的延长线于点F,连接CF.
(1)求证:AD=AF.
(2)当AB=AC=
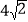 时,求四边形ADCF 的面积.
时,求四边形ADCF 的面积.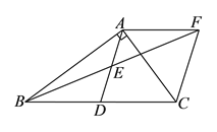
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角
 中,
中, ,
, ,AD,CE分别是
,AD,CE分别是 和
和 的平分线,AD,CE相交于点F.
的平分线,AD,CE相交于点F. 求
求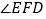 的度数;
的度数; 判断FE与FD之间的数量关系,并证明你的结论.
判断FE与FD之间的数量关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a是最大的负整数,b、c满足
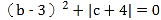 ,且a,b,c分别是点A,B,C在数轴上对应的数.
,且a,b,c分别是点A,B,C在数轴上对应的数.(1)求a,b,c的值,并在数轴上标出点A,B,C;
(2)若动点P从C出发沿数轴正方向运动,点P的速度是每秒2个单位长度,运动几秒后,点P到达B点?
(3)在数轴上找一点M,使点M到A,B,C三点的距离之和等于13,请直接写出所有点M对应的数.(不必说明理由)
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明家买了一辆小轿车,小明连续记录了一周每天行驶的路程:

请你用学过的统计知识解决下面的问题:
(1)小明家的轿车每月(按30天计算)要行驶多少千米?
(2)若每行驶100千米需汽油8升,汽油每升6.64元,请你算出小明家一年(按12个月计算)的汽油费用大约是多少元(精确到百位).
-
科目: 来源: 题型:
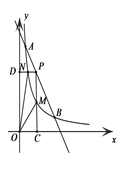
查看答案和解析>>【题目】如图,一次函数与反比例函数的图像交于A(1,12)和B(6,2)两点。点P是线段AB上一动点(不与点A和B重合),过P点分别作x、y轴的垂线PC、PD交反比例函数图像于点M、N,则四边形PMON面积的最大值是( )
A.
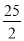 B.
B.  C. 6 D. 12
C. 6 D. 12 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
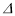 ABC中,AB、BC的垂直平分线相交于三角形内一点O,下列结论中错误的是( )
ABC中,AB、BC的垂直平分线相交于三角形内一点O,下列结论中错误的是( )
A. 点O在AC的垂直平分线上
B.
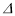 AOB、
AOB、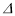 BOC、
BOC、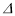 COA都是等腰三角形
COA都是等腰三角形C.
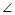 OAB+
OAB+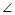 OBC+
OBC+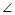 OCA=
OCA=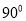
D. 点O到AB、BC、CA的距离相等
相关试题

