【题目】如图,已知∠AOB=140![]() ,∠COE与∠EOD互余,OE平分∠AOD.
,∠COE与∠EOD互余,OE平分∠AOD.
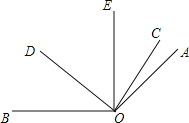
(1)若∠COE=38![]() ,求∠DOE和∠BOD的度数;
,求∠DOE和∠BOD的度数;
(2)设∠COE=α,∠BOD=β,请探究α与β之间的数量关系.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]()
【解析】
(1)根据互余的概念求出∠EOD,根据角平分线的定义求出∠AOD,结合图形计算即可;
(2)根据互余的概念用α表示∠EOD,根据角平分线的定义求出∠AOD,结合图形列式计算即可
(1)∵∠COE与∠EOD互余,![]() ,
,
∴∠EOD=90![]() -38
-38![]() =52
=52![]() ,
,
∵OE平分∠AOD,
∴∠AOD=2∠EOD =104![]() ,
,
∴∠BOD=∠AOB-∠AOD=140![]() -104
-104![]() =36
=36![]() ,
,
故答案为:52![]() ,36
,36![]() ;
;
(2)∵∠COE=![]() ,且∠COE与∠EOD互余,
,且∠COE与∠EOD互余,
∴![]() ,
,
∵OE平分∠AOD,
∴![]() ,
,
∴![]() ,
,
解得:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某企业安排名
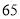 工人生产甲、乙两种产品,每人每天生产
工人生产甲、乙两种产品,每人每天生产 件甲产品或
件甲产品或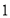 件乙产品,根据市场需求和生产经验,甲产品每件可获利
件乙产品,根据市场需求和生产经验,甲产品每件可获利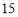 元,乙产品每件可获利
元,乙产品每件可获利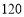 元,而实际生产中,生产乙产品需要额外支出一定的费用,经过核算,每生产
元,而实际生产中,生产乙产品需要额外支出一定的费用,经过核算,每生产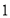 件乙产品,当天平均每件获利减少
件乙产品,当天平均每件获利减少 元,设每天安排
元,设每天安排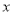 人生产乙产品.
人生产乙产品.  根据信息填表:
根据信息填表:产品种类
每天工人数(人)
每天产量(件)
每件产品可获利润(元)
甲
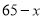
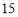
乙
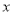
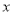
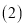 若每天生产甲产品可获得的利润比生产乙产品可获得的利润多
若每天生产甲产品可获得的利润比生产乙产品可获得的利润多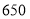 元,试问:该企业每天生产甲、乙产品可获得总利润是多少元?
元,试问:该企业每天生产甲、乙产品可获得总利润是多少元? -
科目: 来源: 题型:
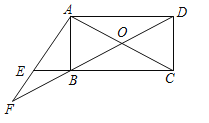
查看答案和解析>>【题目】如图,平行四边形ABCD的对角线AC、BD交于点O,点E在边CB的延长线上,且∠EAC=90°,AE2=EBEC.
(1)求证:四边形ABCD是矩形;
(2)延长DB、AE交于点F,若AF=AC,求证:AE=BF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
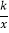 (x<0)的图象经过点A(﹣2,2),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是________.
(x<0)的图象经过点A(﹣2,2),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是________.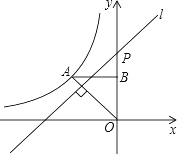
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
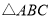 ,
,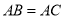 ,
,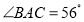 ,
, 的平分线与AB的垂直平分线交于O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与O点恰好重合,则∠OEC的度数为( )
的平分线与AB的垂直平分线交于O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与O点恰好重合,则∠OEC的度数为( )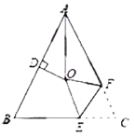
A.
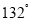 B.
B. 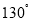 C.
C. 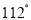 D.
D. 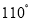
-
科目: 来源: 题型:
查看答案和解析>>【题目】一种商品按销售量分三部分制定销售单价,如下表:
销售量
单价
不超过100件的部分
2.8元/件
超过100件不超过300件的部分
2.2元/件
超过300件的部分
2元/件
(1)若买100件花 元,买300件花 元;买380件花 元;
(2)小明买这种商品花了500元,求购买了这种商品多少件;
(3)若小明花了n元(n>280),恰好购买0.4n件这种商品,求n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(背景知识)数轴上A、B两点在数轴上对应的数为a、b,则A、B两点之间的距离定义为:AB=|b-a|.
(问题情境)已知点A、B、O在数轴上表示的数分别为-6、10和0,点M、N分别从O、B出发,同时向左匀速运动,点M的速度是每秒1个单位长度,点N的速度是每秒3个单位长度,设运动的时间为t秒(t>0),
(1)填空:①OA= .OB= ;
②用含t的式子表示:AM= ;AN= ;
(2)当t为何值时,恰好有AN=2AM;
(3)求|t-6|+|t+10|的最小值.
相关试题

