【题目】(背景知识)数轴上A、B两点在数轴上对应的数为a、b,则A、B两点之间的距离定义为:AB=|b-a|.
(问题情境)已知点A、B、O在数轴上表示的数分别为-6、10和0,点M、N分别从O、B出发,同时向左匀速运动,点M的速度是每秒1个单位长度,点N的速度是每秒3个单位长度,设运动的时间为t秒(t>0),
(1)填空:①OA= .OB= ;
②用含t的式子表示:AM= ;AN= ;
(2)当t为何值时,恰好有AN=2AM;
(3)求|t-6|+|t+10|的最小值.
参考答案:
【答案】(1)①6,10;②![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() ;(3)16
;(3)16
【解析】
(1)①根据两点之间的距离定义,即可求出线段OA、OB的长;
②根据两点之间的距离定义,即可得出线段![]() 、
、![]() 的长;
的长;
(2)根据②的结论,列方程并解方程即可;
(3)分成不重复且不遗漏的三种情况解答即可得到结果.
(1)①∵点A、B在数轴上对应的数为-6、10,
∴![]() ,
,
故答案为:6,10;
②根据题意得:M点表示的数为:![]() ,N点表示的数为:
,N点表示的数为:![]() ,
,
则:![]() ,
,
故答案为:![]() ,
,![]() ;
;
(2)∵![]() ,
,
∴![]() ,
,
则![]() ,
,
解得:![]() 或
或![]() ;
;
(3)当![]() 时,
时,![]() ,没有最小值;
,没有最小值;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,没有最小值;
,没有最小值;
综上,![]() 的最小值为
的最小值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠AOB=140
 ,∠COE与∠EOD互余,OE平分∠AOD.
,∠COE与∠EOD互余,OE平分∠AOD.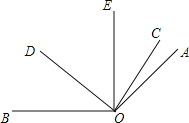
(1)若∠COE=38
 ,求∠DOE和∠BOD的度数;
,求∠DOE和∠BOD的度数;(2)设∠COE=α,∠BOD=β,请探究α与β之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
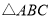 ,
,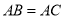 ,
,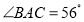 ,
,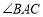 的平分线与AB的垂直平分线交于O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与O点恰好重合,则∠OEC的度数为( )
的平分线与AB的垂直平分线交于O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与O点恰好重合,则∠OEC的度数为( )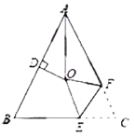
A.
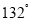 B.
B. 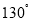 C.
C. 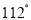 D.
D. 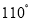
-
科目: 来源: 题型:
查看答案和解析>>【题目】一种商品按销售量分三部分制定销售单价,如下表:
销售量
单价
不超过100件的部分
2.8元/件
超过100件不超过300件的部分
2.2元/件
超过300件的部分
2元/件
(1)若买100件花 元,买300件花 元;买380件花 元;
(2)小明买这种商品花了500元,求购买了这种商品多少件;
(3)若小明花了n元(n>280),恰好购买0.4n件这种商品,求n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点 O 是直线 AB上一点,∠COD 是直角,OE平分∠BOC.
(1)①如图1,若∠DOE=25°,求∠AOC 的度数;
②如图2,若∠DOE=α,直接写出∠AOC的度数(用含α的式子表示);
(2)将图 1中的∠COD 绕点O按顺时针方向旋转至图 2 所示位置.探究∠DOE 与∠AOC 的度数之间的关系,写出你的结论,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为6的正三角形纸片ABC按如下顺序进行两次折叠,展平后,得折痕AD,BE(如图①),点O为其交点.
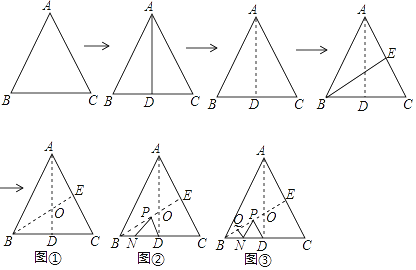
(1)探求AO到OD的数量关系,并说明理由;
(2)如图②,若P,N分别为BE,BC上的动点.
(Ⅰ)当PN+PD的长度取得最小值时,求BP的长度;
(Ⅱ)如图③,若点Q在线段BO上,BQ=1,则QN+NP+PD的最小值= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线l:y=(x﹣h)2﹣4(h为常数)
(1)如图1,当抛物线l恰好经过点P(1,﹣4)时,l与x轴从左到右的交点为A、B,与y轴交于点C.
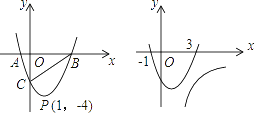
①求l的解析式,并写出l的对称轴及顶点坐标.
②在l上是否存在点D,使S△ABD=S△ABC , 若存在,请求出D点坐标,若不存在,请说明理由.
③点M是l上任意一点,过点M做ME垂直y轴于点E,交直线BC于点D,过点D作x轴的垂线,垂足为F,连接EF,当线段EF的长度最短时,求出点M的坐标.
(2)设l与双曲线y=
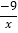 有个交点横坐标为x0,且满足3≤x0≤5,通过l位置随h变化的过程,直接写出h的取值范围.
有个交点横坐标为x0,且满足3≤x0≤5,通过l位置随h变化的过程,直接写出h的取值范围.
相关试题

