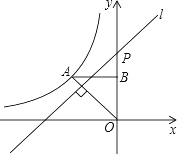
【题目】如图,反比例函数y=![]() (x<0)的图象经过点A(﹣2,2),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是________.
(x<0)的图象经过点A(﹣2,2),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是________.
参考答案:
【答案】1+![]()
【解析】根据反比例函数图象上点的坐标特征由A点坐标为(-2,2)得到k=-4,即反比例函数解析式为y=-![]() ,且OB=AB=2,则可判断△OAB为等腰直角三角形,所以∠AOB=45°,再利用PQ⊥OA可得到∠OPQ=45°,然后由轴对称的性质得PB=PB′,BB′⊥PQ,所以∠BPQ=∠B′PQ=45°,于是得到B′P⊥y轴,则点B′的坐标可表示为(-
,且OB=AB=2,则可判断△OAB为等腰直角三角形,所以∠AOB=45°,再利用PQ⊥OA可得到∠OPQ=45°,然后由轴对称的性质得PB=PB′,BB′⊥PQ,所以∠BPQ=∠B′PQ=45°,于是得到B′P⊥y轴,则点B′的坐标可表示为(-![]() ,t),于是利用PB=PB′得t-2=|-
,t),于是利用PB=PB′得t-2=|-![]() |=
|=![]() ,然后解方程可得到满足条件的t的值.
,然后解方程可得到满足条件的t的值.
∵点A坐标为(-2,2),
∴k=-2×2=-4,
∴反比例函数解析式为y=-![]() ,
,
∵OB=AB=2,
∴△OAB为等腰直角三角形,
∴∠AOB=45°,
∵PQ⊥OA,
∴∠OPQ=45°,
∵点B和点B′关于直线l对称,
∴PB=PB′,BB′⊥PQ,
∴∠B′PQ=∠OPQ=45°,∠B′PB=90°,
∴B′P⊥y轴,
∴点B′的坐标为(-![]() ,t),
,t),
∵PB=PB′,
∴t-2=|-![]() |=
|=![]() ,
,
整理得t2-2t-4=0,解得t1=1+![]() ,t2=1-
,t2=1-![]() (不符合题意,舍去),
(不符合题意,舍去),
∴t的值为1+![]() ,
,
故答案为:1+![]() .
.

-
科目: 来源: 题型:
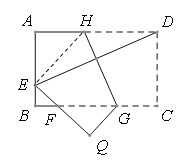
查看答案和解析>>【题目】如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在AB边上E处,EQ与BC相交于F,若AD=8 cm,AB=6 cm,AE=4cm,则△EBF的周长是______________ cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某企业安排名
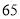 工人生产甲、乙两种产品,每人每天生产
工人生产甲、乙两种产品,每人每天生产 件甲产品或
件甲产品或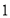 件乙产品,根据市场需求和生产经验,甲产品每件可获利
件乙产品,根据市场需求和生产经验,甲产品每件可获利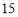 元,乙产品每件可获利
元,乙产品每件可获利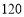 元,而实际生产中,生产乙产品需要额外支出一定的费用,经过核算,每生产
元,而实际生产中,生产乙产品需要额外支出一定的费用,经过核算,每生产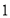 件乙产品,当天平均每件获利减少
件乙产品,当天平均每件获利减少 元,设每天安排
元,设每天安排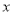 人生产乙产品.
人生产乙产品. 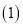 根据信息填表:
根据信息填表:产品种类
每天工人数(人)
每天产量(件)
每件产品可获利润(元)
甲
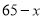
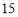
乙
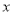
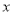
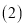 若每天生产甲产品可获得的利润比生产乙产品可获得的利润多
若每天生产甲产品可获得的利润比生产乙产品可获得的利润多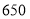 元,试问:该企业每天生产甲、乙产品可获得总利润是多少元?
元,试问:该企业每天生产甲、乙产品可获得总利润是多少元? -
科目: 来源: 题型:
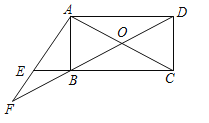
查看答案和解析>>【题目】如图,平行四边形ABCD的对角线AC、BD交于点O,点E在边CB的延长线上,且∠EAC=90°,AE2=EBEC.
(1)求证:四边形ABCD是矩形;
(2)延长DB、AE交于点F,若AF=AC,求证:AE=BF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠AOB=140
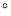 ,∠COE与∠EOD互余,OE平分∠AOD.
,∠COE与∠EOD互余,OE平分∠AOD.
(1)若∠COE=38
 ,求∠DOE和∠BOD的度数;
,求∠DOE和∠BOD的度数;(2)设∠COE=α,∠BOD=β,请探究α与β之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
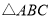 ,
,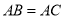 ,
,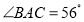 ,
,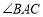 的平分线与AB的垂直平分线交于O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与O点恰好重合,则∠OEC的度数为( )
的平分线与AB的垂直平分线交于O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与O点恰好重合,则∠OEC的度数为( )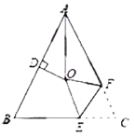
A.
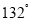 B.
B. 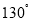 C.
C. 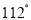 D.
D. 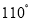
-
科目: 来源: 题型:
查看答案和解析>>【题目】一种商品按销售量分三部分制定销售单价,如下表:
销售量
单价
不超过100件的部分
2.8元/件
超过100件不超过300件的部分
2.2元/件
超过300件的部分
2元/件
(1)若买100件花 元,买300件花 元;买380件花 元;
(2)小明买这种商品花了500元,求购买了这种商品多少件;
(3)若小明花了n元(n>280),恰好购买0.4n件这种商品,求n的值.
相关试题

