【题目】如图,![]() ,
,![]() ,
,![]() ,
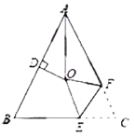
,![]() 的平分线与AB的垂直平分线交于O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与O点恰好重合,则∠OEC的度数为( )
的平分线与AB的垂直平分线交于O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与O点恰好重合,则∠OEC的度数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】C
【解析】
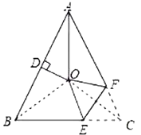
连接OB、OC,根据角平分线的定义求出∠BAO,根据等腰三角形两底角相等求出∠ABC,再根据线段垂直平分线上的点到线段两端点的距离相等可得OA=OB,根据等边对等角可得∠ABO=∠BAO,再求出∠OBC,然后判断出点O是△ABC的外心,根据三角形外心的性质可得OB=OC,再根据等边对等角求出∠OCB=∠OBC,根据翻折的性质可得OE=CE,然后根据等边对等角求出∠COE,再利用三角形内角和定理列式计算即可得出答案.
如图,连接OB、OC,
∵![]() ,AO为
,AO为![]() 的平分线
的平分线
∴![]()
又∵![]() ,
,
∴![]()
∵DO是AB的垂直平分线,
∴![]() .
.
∴![]() ,
,
∴![]()
∵DO是AB的垂直平分线,AO为![]() 的平分线
的平分线
∴点О是![]() 的外心,
的外心,
∴![]() ,
,
∴![]() ,
,
∵将![]() 沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合
沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]()
-
科目: 来源: 题型:
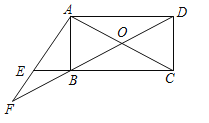
查看答案和解析>>【题目】如图,平行四边形ABCD的对角线AC、BD交于点O,点E在边CB的延长线上,且∠EAC=90°,AE2=EBEC.
(1)求证:四边形ABCD是矩形;
(2)延长DB、AE交于点F,若AF=AC,求证:AE=BF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
 (x<0)的图象经过点A(﹣2,2),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是________.
(x<0)的图象经过点A(﹣2,2),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是________.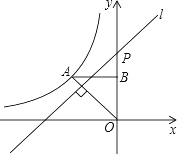
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠AOB=140
 ,∠COE与∠EOD互余,OE平分∠AOD.
,∠COE与∠EOD互余,OE平分∠AOD.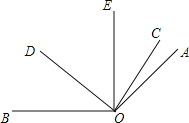
(1)若∠COE=38
 ,求∠DOE和∠BOD的度数;
,求∠DOE和∠BOD的度数;(2)设∠COE=α,∠BOD=β,请探究α与β之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一种商品按销售量分三部分制定销售单价,如下表:
销售量
单价
不超过100件的部分
2.8元/件
超过100件不超过300件的部分
2.2元/件
超过300件的部分
2元/件
(1)若买100件花 元,买300件花 元;买380件花 元;
(2)小明买这种商品花了500元,求购买了这种商品多少件;
(3)若小明花了n元(n>280),恰好购买0.4n件这种商品,求n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(背景知识)数轴上A、B两点在数轴上对应的数为a、b,则A、B两点之间的距离定义为:AB=|b-a|.
(问题情境)已知点A、B、O在数轴上表示的数分别为-6、10和0,点M、N分别从O、B出发,同时向左匀速运动,点M的速度是每秒1个单位长度,点N的速度是每秒3个单位长度,设运动的时间为t秒(t>0),
(1)填空:①OA= .OB= ;
②用含t的式子表示:AM= ;AN= ;
(2)当t为何值时,恰好有AN=2AM;
(3)求|t-6|+|t+10|的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点 O 是直线 AB上一点,∠COD 是直角,OE平分∠BOC.
(1)①如图1,若∠DOE=25°,求∠AOC 的度数;
②如图2,若∠DOE=α,直接写出∠AOC的度数(用含α的式子表示);
(2)将图 1中的∠COD 绕点O按顺时针方向旋转至图 2 所示位置.探究∠DOE 与∠AOC 的度数之间的关系,写出你的结论,并说明理由.

相关试题

