【题目】我市某企业安排名![]() 工人生产甲、乙两种产品,每人每天生产
工人生产甲、乙两种产品,每人每天生产![]() 件甲产品或
件甲产品或![]() 件乙产品,根据市场需求和生产经验,甲产品每件可获利
件乙产品,根据市场需求和生产经验,甲产品每件可获利![]() 元,乙产品每件可获利
元,乙产品每件可获利![]() 元,而实际生产中,生产乙产品需要额外支出一定的费用,经过核算,每生产
元,而实际生产中,生产乙产品需要额外支出一定的费用,经过核算,每生产![]() 件乙产品,当天平均每件获利减少
件乙产品,当天平均每件获利减少![]() 元,设每天安排
元,设每天安排![]() 人生产乙产品.
人生产乙产品.
![]() 根据信息填表:
根据信息填表:
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 |
|
| |
乙 |
|
|
![]() 若每天生产甲产品可获得的利润比生产乙产品可获得的利润多
若每天生产甲产品可获得的利润比生产乙产品可获得的利润多![]() 元,试问:该企业每天生产甲、乙产品可获得总利润是多少元?
元,试问:该企业每天生产甲、乙产品可获得总利润是多少元?
参考答案:
【答案】(1)2(65x),1202x;(2)该企业每天生产甲、乙产品可获得总利润是2650元.
【解析】
(1)设每天安排x人生产乙产品,则每天安排(65x)人生产甲产品,每天可生产x件乙产品,每件的利润为(1202x)元,每天可生产2(65x)件甲产品,此问得解;
(2)由总利润=每件产品的利润×生产数量,结合每天生产甲产品可获得的利润比生产乙产品可获得的利润多650元,即可得出关于x的一元二次方程,解之取其较小值得到x值,然后再计算总利润即可.
解:(1)设每天安排x人生产乙产品,则每天安排(65x)人生产甲产品,每天可生产x件乙产品,每件的利润为(1202x)元,每天可生产2(65x)件甲产品.
填表如下:
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 |
| 2(65x) |
|
乙 |
|
| 1202x |
(2)依题意,得:15×2(65x)(1202x)x=650,
整理得:x275x+650=0
解得:x1=10,x2=65(不合题意,舍去),
∴15×2(65x)+(1202x)x=2650.
答:该企业每天生产甲、乙产品可获得总利润是2650元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=8,AC=6.点D在边AB上,AD=4.5.△ABC的角平分线AE交CD于点F.
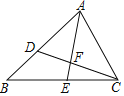
(1)求证:△ACD∽△ABC;
(2)求
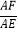 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,有一长方形的空地,长为
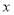 米,宽为
米,宽为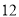 米,建筑商把它分成甲、乙、丙三部分,甲和乙为正方形.现计划甲建筑成住宅区,乙建成商场丙开辟成公园.
米,建筑商把它分成甲、乙、丙三部分,甲和乙为正方形.现计划甲建筑成住宅区,乙建成商场丙开辟成公园.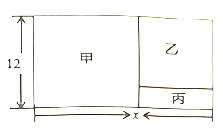
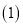 请用含
请用含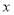 的代数式表示正方形乙的边长; ;
的代数式表示正方形乙的边长; ;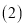 若丙地的面积为
若丙地的面积为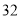 平方米,请求出
平方米,请求出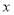 的值.
的值. -
科目: 来源: 题型:
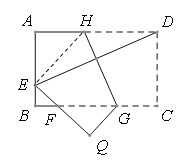
查看答案和解析>>【题目】如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在AB边上E处,EQ与BC相交于F,若AD=8 cm,AB=6 cm,AE=4cm,则△EBF的周长是______________ cm.
-
科目: 来源: 题型:
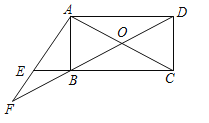
查看答案和解析>>【题目】如图,平行四边形ABCD的对角线AC、BD交于点O,点E在边CB的延长线上,且∠EAC=90°,AE2=EBEC.
(1)求证:四边形ABCD是矩形;
(2)延长DB、AE交于点F,若AF=AC,求证:AE=BF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
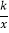 (x<0)的图象经过点A(﹣2,2),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是________.
(x<0)的图象经过点A(﹣2,2),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是________.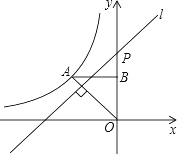
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠AOB=140
 ,∠COE与∠EOD互余,OE平分∠AOD.
,∠COE与∠EOD互余,OE平分∠AOD.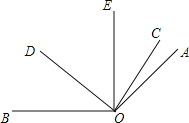
(1)若∠COE=38
 ,求∠DOE和∠BOD的度数;
,求∠DOE和∠BOD的度数;(2)设∠COE=α,∠BOD=β,请探究α与β之间的数量关系.
相关试题

