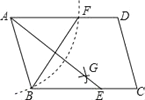
【题目】如图,在□ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=6,AB=5,则AE的长为____.
参考答案:
【答案】8
【解析】
由基本作图得到AB=AF,加上AO平分∠BAD,则根据等腰三角形的性质得到AO⊥BF,BO=FO=![]() BF=3,再根据平行四边形的性质得AF∥BE,所以∠1=∠3,于是得到∠2=∠3,根据等腰三角形的判定得AB=EB,然后再根据等腰三角形的性质得到AO=OE,最后利用勾股定理计算出AO,从而得到AE的长.
BF=3,再根据平行四边形的性质得AF∥BE,所以∠1=∠3,于是得到∠2=∠3,根据等腰三角形的判定得AB=EB,然后再根据等腰三角形的性质得到AO=OE,最后利用勾股定理计算出AO,从而得到AE的长.
解:连结EF,AE与BF交于点O,如图,
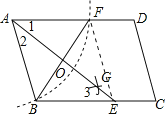
∵AB=AF,AO平分∠BAD,
∴AO⊥BF,BO=FO=![]() BF=3,
BF=3,
∵四边形ABCD为平行四边形,
∴AF∥BE,
∴∠1=∠3,
∴∠2=∠3,
∴AB=EB,
而BO⊥AE,
∴AO=OE,
在Rt△AOB中,AO=![]() =4,
=4,
∴AE=2AO=8.
故答案为:8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在物理实验中,当电流在一定时间段内正常通过电子元件时,每个电子元件的状态有两种可能:通电或断开,并且这两种状态的可能性相等.
(1)如图1,当有2个电子元件
 并联时,请你用树状图表示图中
并联时,请你用树状图表示图中 之间电流能否通过的所有可能情况,并求出
之间电流能否通过的所有可能情况,并求出 之间电流通过的概率;
之间电流通过的概率;(2)如图2,当有3个电子元件并联时,求
 之间电流通过的概率.
之间电流通过的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1.正方形ABCD,过点A作∠EAF=90°,两边分别交直线BC于点E,交线段CD于点F,G为AE中点,连接BG
(1)求证:△ABE≌△ADF
(2)如图2,过点G作BG的垂线交对角线AC于点H,求证:GH=GB;
(3)如图3,连接HF,若CH=3AH,AD=2
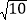 ,求线段HF的长.
,求线段HF的长.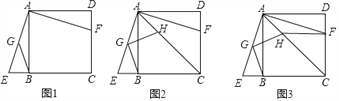
-
科目: 来源: 题型:
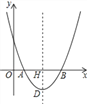
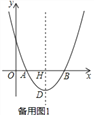
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2﹣10ax+16a(a≠0)交x轴于A、B两点,抛物线的顶点为D,对称轴与x轴交于点H,且AB=2DH.
(1)求a的值;
(2)点P是对称轴右侧抛物线上的点,连接PD,PQ⊥x轴于点Q,点N是线段PQ上的点,过点N作NF⊥DH于点F,NE⊥PD交直线DH于点E,求线段EF的长;
(3)在(2)的条件下,连接DN、DQ、PB,当DN=2QN(NQ>3),2∠NDQ+∠DNQ=90°时,作NC⊥PB交对称轴左侧的抛物线于点C,求点C的坐标.
-
科目: 来源: 题型:
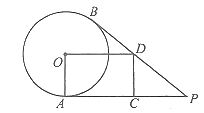
查看答案和解析>>【题目】已知:如图,点
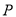 是
是 外一点,过点
外一点,过点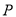 分别作
分别作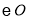 的切线
的切线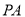 、
、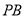 ,切点为点
,切点为点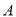 、
、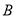 ,连接
,连接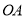 ,过点
,过点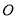 作
作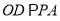 交
交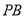 于点
于点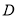 ,过点
,过点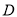 作
作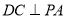 于
于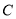 .
.(1)求证:四边形
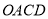 是矩形;
是矩形;(2)若
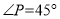 ,
, 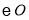 的半径为
的半径为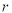 ,试证明四边形
,试证明四边形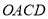 的周长等于
的周长等于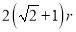 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,点E是BC的中点,点F在AD上,AF=6cm,BF=12cm,BD平分∠FBC,若点P,Q分别是AF,BC上点,且CQ=2AP.若点P、Q、E、F为顶点的四边形构成平行四边形,则AP的长为______.
中,点E是BC的中点,点F在AD上,AF=6cm,BF=12cm,BD平分∠FBC,若点P,Q分别是AF,BC上点,且CQ=2AP.若点P、Q、E、F为顶点的四边形构成平行四边形,则AP的长为______.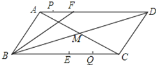
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E.
(1)求证:四边形CODE是矩形.
(2)若AB=5,AC=6,求四边形CODE的周长.

相关试题

