【题目】在物理实验中,当电流在一定时间段内正常通过电子元件时,每个电子元件的状态有两种可能:通电或断开,并且这两种状态的可能性相等.
(1)如图1,当有2个电子元件![]() 并联时,请你用树状图表示图中
并联时,请你用树状图表示图中![]() 之间电流能否通过的所有可能情况,并求出
之间电流能否通过的所有可能情况,并求出![]() 之间电流通过的概率;
之间电流通过的概率;
(2)如图2,当有3个电子元件并联时,求![]() 之间电流通过的概率.
之间电流通过的概率.

参考答案:
【答案】![]() 之间电流通过的概率是
之间电流通过的概率是![]() ;(2)
;(2)![]() 之间电流通过的概率是
之间电流通过的概率是![]() .
.
【解析】试题分析:
(1)由题意画出树状图找到所有的等可能事件,结合并联电路的知识求出对应的概率即可;
(2)由题意画出树状图找到所有的等可能事件,结合并联电路的知识求出对应的概率即可;
试题解析:
(1)用树状图表示为:
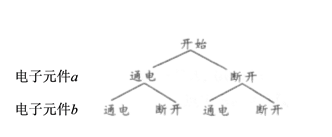
由图可知,共有4种等可能结果,其中P、Q间没有电流通过的只有1种,有电流通过的有3种,
∴![]() 之间电流通过的概率是
之间电流通过的概率是![]() ;
;
(2)画树状图得:
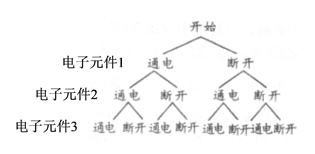
由图可知,共有8种等可能结果,其中没有电流通过的只有1种,有电流通过的有7种,
∴![]() 之间电流通过的概率是
之间电流通过的概率是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )

A. BE=DF B. BF=DE C. AE=CF D. ∠1=∠2
-
科目: 来源: 题型:
查看答案和解析>>【题目】类比学习:一动点沿着数轴先向右平移3个单位长度,再向左平移2个单位长度,相当于向右平移1个单位长度.用实数加法表示为3+(-2)=1.若坐标平面上的点有如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移|a|个单位长度),沿y轴方向平移的数量为b(向上为正,向下为负,平移|b|个单位长度),则把有序数对{a,b}叫做这一平移的“平移量”,“平移量”{a,b}与“平移量”{c,d}的加法运算法则为{a,b}+{c,d}={a+c,b+d}.
解决问题:
(1)计算:{3,1}+{1,2},{1,2}+{3,1}.
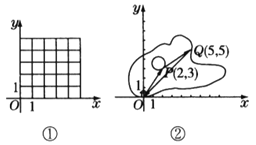
(2)动点P从坐标原点O出发,先按照“平移量”{3,1}平移到点A,再按照“平移量”{1,2}平移到点B;若先把动点P按照“平移量”{1,2}平移到点C,再按照“平移量”{3,1}平移,最后的位置还是点B吗?在图①中画出四边形OABC.
(3)如图②所示,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O.请用“平移量”加法算式表示它的航行过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图中的图象(折线ABCDE)描述了一汽车在某一直道上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系.根据图中提供的信息,给出下列说法:
①汽车共行驶了120千米;
②汽车在行驶途中停留了0.5小时;
③汽车在整个行驶过程中的平均速度为
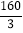 千米/时;
千米/时;④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少.
其中正确的说法有( )
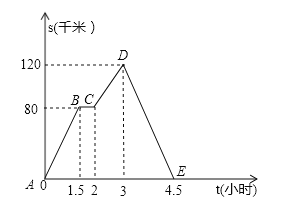
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1.正方形ABCD,过点A作∠EAF=90°,两边分别交直线BC于点E,交线段CD于点F,G为AE中点,连接BG
(1)求证:△ABE≌△ADF
(2)如图2,过点G作BG的垂线交对角线AC于点H,求证:GH=GB;
(3)如图3,连接HF,若CH=3AH,AD=2
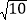 ,求线段HF的长.
,求线段HF的长.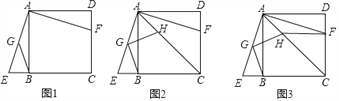
-
科目: 来源: 题型:
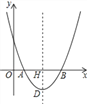
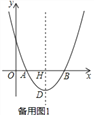
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2﹣10ax+16a(a≠0)交x轴于A、B两点,抛物线的顶点为D,对称轴与x轴交于点H,且AB=2DH.
(1)求a的值;
(2)点P是对称轴右侧抛物线上的点,连接PD,PQ⊥x轴于点Q,点N是线段PQ上的点,过点N作NF⊥DH于点F,NE⊥PD交直线DH于点E,求线段EF的长;
(3)在(2)的条件下,连接DN、DQ、PB,当DN=2QN(NQ>3),2∠NDQ+∠DNQ=90°时,作NC⊥PB交对称轴左侧的抛物线于点C,求点C的坐标.
-
科目: 来源: 题型:
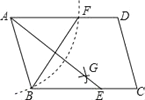
查看答案和解析>>【题目】如图,在□ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=6,AB=5,则AE的长为____.
相关试题

