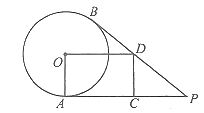
【题目】已知:如图,点![]() 是
是![]() 外一点,过点
外一点,过点![]() 分别作
分别作![]() 的切线
的切线![]() 、
、![]() ,切点为点
,切点为点![]() 、
、![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于
于![]() .
.
(1)求证:四边形![]() 是矩形;
是矩形;
(2)若![]() ,
, ![]() 的半径为
的半径为![]() ,试证明四边形
,试证明四边形![]() 的周长等于
的周长等于![]() .
.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:
(1)由PA是![]() 的切线可得∠OAP=90°,结合OD∥AP可得∠O=90°,再结合DC⊥AP即可得到四边形OACD矩形了;
的切线可得∠OAP=90°,结合OD∥AP可得∠O=90°,再结合DC⊥AP即可得到四边形OACD矩形了;
(2)如图,连接OB,由四边形AOCD是矩形结合![]() 的半径为
的半径为![]() 可得DC=OA=OB=
可得DC=OA=OB= ![]() ,由OD∥AP可得∠BDO=∠P=45°,由PB是
,由OD∥AP可得∠BDO=∠P=45°,由PB是![]() 的切线可得∠OBD=90°,由此可得BD=OB=r,则OD=
的切线可得∠OBD=90°,由此可得BD=OB=r,则OD= ![]() =AC,这样即可由OA+AC+DC+OD求得四边形OACD的周长为
=AC,这样即可由OA+AC+DC+OD求得四边形OACD的周长为![]() .
.
试题解析:
(1)∵![]() 是
是![]() 的切线,切点为
的切线,切点为![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴四边形![]() 是矩形;
是矩形;
(2)如图,连接OB,
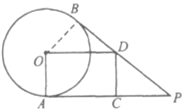
由(1)得,四边形![]() 是矩形,
是矩形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 的切线,
的切线,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,由勾股定理得:
中,由勾股定理得: ![]() ,
,
∴四边形![]() 的周长
的周长![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1.正方形ABCD,过点A作∠EAF=90°,两边分别交直线BC于点E,交线段CD于点F,G为AE中点,连接BG
(1)求证:△ABE≌△ADF
(2)如图2,过点G作BG的垂线交对角线AC于点H,求证:GH=GB;
(3)如图3,连接HF,若CH=3AH,AD=2
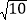 ,求线段HF的长.
,求线段HF的长.
-
科目: 来源: 题型:
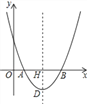
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2﹣10ax+16a(a≠0)交x轴于A、B两点,抛物线的顶点为D,对称轴与x轴交于点H,且AB=2DH.
(1)求a的值;
(2)点P是对称轴右侧抛物线上的点,连接PD,PQ⊥x轴于点Q,点N是线段PQ上的点,过点N作NF⊥DH于点F,NE⊥PD交直线DH于点E,求线段EF的长;
(3)在(2)的条件下,连接DN、DQ、PB,当DN=2QN(NQ>3),2∠NDQ+∠DNQ=90°时,作NC⊥PB交对称轴左侧的抛物线于点C,求点C的坐标.
-
科目: 来源: 题型:
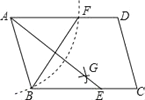
查看答案和解析>>【题目】如图,在□ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=6,AB=5,则AE的长为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
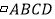 中,点E是BC的中点,点F在AD上,AF=6cm,BF=12cm,BD平分∠FBC,若点P,Q分别是AF,BC上点,且CQ=2AP.若点P、Q、E、F为顶点的四边形构成平行四边形,则AP的长为______.
中,点E是BC的中点,点F在AD上,AF=6cm,BF=12cm,BD平分∠FBC,若点P,Q分别是AF,BC上点,且CQ=2AP.若点P、Q、E、F为顶点的四边形构成平行四边形,则AP的长为______.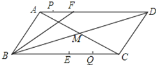
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E.
(1)求证:四边形CODE是矩形.
(2)若AB=5,AC=6,求四边形CODE的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上的A、B两点分别对应数字a、b,且a、b满足|4a-b|+(a-4)2=0

(1)a= ,b= ,并在数轴上面出A、B两点;
(2)若点P从点A出发,以每秒3个单位长度向x轴正半轴运动,求运动时间为多少时,点P到点A的距离是点P到点B距离的2倍;
(3)数轴上还有一点C的坐标为30,若点P和点Q同时从点A和点B出发,分别以每秒3个单位长度和每秒1个单位长度的速度向C点运动,P点到达C点后,再立刻以同样的速度返回,运动到终点A.求点P和点Q运动多少秒时,P、Q两点之间的距离为4,并求此时点Q对应的数.
相关试题

