【题目】砀山酥梨是一种驰名中外的特色水果,它是梨的一种,因为出产于砀山县而得名。现有20筐砀山酥梨,以每筐25千克的质量为标准,超过或不足的千克数分别用正、负数来表示,记录如下:

(1)这20筐砀山酥梨中,最重的一筐比最轻的一筐重多少千克?
(2)与标准质量比较,这20筐砀山酥梨总计超过或不足多少千克?
(3)若砀山酥梨每千克售价4元,则这20筐砀山酥梨可卖多少元?
参考答案:
【答案】(1)答:最重的一筐比最轻的一筐重5.5千克;(2)这20筐砀山酥梨总计超过8千克;(3)这20筐砀山酥梨可卖2032元.
【解析】
(1)由题意用与标准质量的最大差值减去与标准质量的最小差值即可得到结果;
(2)把表中所有与标准质量的差值相加即可得到结果;
(3)先求出这20筐砀山酥梨的总质量,再乘以4即可得到结果.
(1)2.5-(-3)=5.5(千克)
答:最重的一筐比最轻的一筐重5.5千克.
(2)(-3)×1+(-2)×4+(-1.5)×2+1×2+2.5×8=8(千克)
答:这20筐砀山酥梨总计超过8千克.
(3)20×25+8=508(千克) 508×4=2032(元)
答:这20筐砀山酥梨可卖2032元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(4,0),B(0,﹣4),C(a,2a)及点D是一个平行四边形的四个顶点,则线段CD的长的最小值为( )
A.
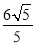 B.
B. 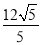 C.
C. 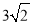 D.
D. 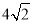
-
科目: 来源: 题型:
查看答案和解析>>【题目】感知:如图①,∠C=∠ABD=∠E=90°,可知△ACB∽△BED.(不要求证明)
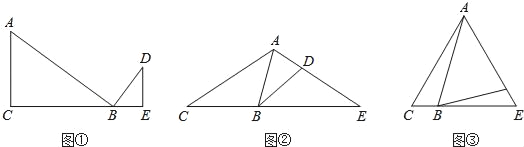
拓展:如图②,∠C=∠ABD=∠E.求证:△ACB∽△BED.
应用:如图③,∠C=∠ABD=∠E=60°,AC=4,BC=1,则△ABD与△BDE的面积比为
.
-
科目: 来源: 题型:
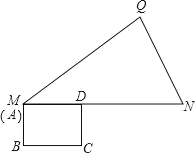
查看答案和解析>>【题目】如图,在△MNQ中,MN=11,NQ=
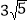 ,
,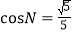 ,矩形ABCD,BC=4,CD=3,点A与M重合,AD与MN重合.矩形ABCD沿着MQ方向平移,且平移速度为每秒5个单位,当点A与Q重合时停止运动.
,矩形ABCD,BC=4,CD=3,点A与M重合,AD与MN重合.矩形ABCD沿着MQ方向平移,且平移速度为每秒5个单位,当点A与Q重合时停止运动.(1)MQ的长度是 ;
(2)运动 秒,BC与MN重合;
(3)设矩形ABCD与△MNQ重叠部分的面积为S,运动时间为t,求出S与t之间的函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复上述过程,下表是活动进行中的一组统计数据:
摸球的次数n
100
150
200
500
800
1000
摸到白球的次数m
58
96
116
295
484
601
摸到白球的频率
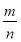
0.64
0.58
0.605
0.601
(1)请将表中的数据补充完整,
(2)请估计:当n很大时,摸到白球的概率约是 .(精确到0.1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:若一个关于x的方程
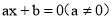 的解为
的解为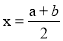 ,则称此方程为“中点方程”.如:
,则称此方程为“中点方程”.如: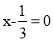 的解为
的解为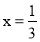 ,而
,而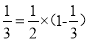 ;
;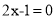 的解为
的解为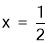 ,而
,而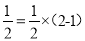 .
.(1)若
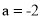 ,有符合要求的“中点方程”吗?若有,请求出该方程的解;若没有请说明理由;
,有符合要求的“中点方程”吗?若有,请求出该方程的解;若没有请说明理由;(2)若关于x的方程
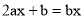 是“中点方程”,求代数式
是“中点方程”,求代数式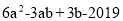 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】把所有正偶数从小到大排列,并按如下规律分组:
第一组:2,4;
第二组:6,8,10,12;
第三组:14,16,18,20,22,24
第四组:26,28,30,32,34,36,38,40
……
则现有等式Am=(i,j)表示正偶数m是第i组第j个数(从左到右数),如A10=(2,3),则A2018=( )
A. (31,63) B. (32,17) C. (33,16) D. (34,2)
相关试题

