【题目】已知:AB是⊙O的直径,DA、DC分别是⊙O的切线,点A、C是切点,连接DO交弧AC于点E,连接AE、CE.
(1)如图1,求证:EA=EC;
(2)如图2,延长DO交⊙O于点F,连接CF、BE交于点G,求证:∠CGE=2∠F;
(3)如图3,在(2)的条件下,DE=![]() AD,EF=2
AD,EF=2![]() , 求线段CG的长.
, 求线段CG的长.
参考答案:
【答案】证明:(1)如图1,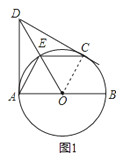
连接OC,
∵DA、DC分别是⊙O的切线,点A、C是切点,OA、OC是半径,
∴OA⊥DA,OC⊥DC,
∴∠DAO=∠DCO=90°,
在Rt△ODA和Rt△ODC中,![]() ,
,
∴Rt△ODA≌Rt△ODC,
∴∠EOA=∠EOC,
∴AE=CE;
(2)证明:如图2,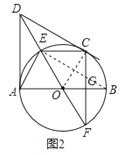
连接OC,BE,由(1)证得∠AOE=∠COE,
又∵∠B=![]() ∠AOE,∠F=
∠AOE,∠F=![]() ∠COE,
∠COE,
∴∠B=∠F,
∵OB=OE,
∴∠B=∠OEB,
∴∠F=∠OEG,
∵∠EGC是△EGF的外角,
∴∠EGC=∠F+∠GEF=2∠F,
即∠EGC=2∠F;
(3)解:∵EF是⊙O的直径,
∴∠ECF=90°
∵EF=2![]() ,
,
∴OA=OE=![]() EF=
EF=![]() ,
,
∵DE=![]() AD,设DE=m,
AD,设DE=m,
∴AD=2m,
在Rt△DAO中,OA2+DA2=OD2 ,
∴![]() ,
,
解得m1=0(舍去),m2=![]() ,
,
∴DA=![]()
![]() ,DO=
,DO=![]()
![]() ,
,
∴在Rt△ADO中,tan∠DOA=![]() =
=![]() ,cos∠DOA=
,cos∠DOA=![]() =
=![]() ,
,
∵∠EOA=2∠B,∠EGC=2∠F,
∴∠EGC=∠EOA,
∴tan∠EGC=![]() ,
,
如图3,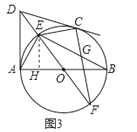
过点E作EH⊥AB于点H,
在Rt△EOH中OH=OEcos∠EOH=![]() X
X![]() =
=![]()
![]() ,
,
∴EH=![]()
![]() AH=AO﹣OH=
AH=AO﹣OH=![]() -
-![]()
![]() =
=![]()
![]() ,
,
在Rt△EHA中,EA2=AH2+EH2 ,
∴EA=2,
∵AE=CE,
∴EC=2,
在Rt△ECG中,tan∠EGC=![]() =
=![]() =
=![]() ,
,
∴GC=![]() .
.
【解析】(1)连接OC,根据切线的性质得到OA⊥DA,OC⊥DC,由垂直的定义得到∠DAO=∠DCO=90°,推出Rt△ODA≌Rt△ODC,根据全等三角形的性质得到∠EOA=∠EOC,由等腰三角形的判定得到结论;
(2)连接OC,BE,由(1)证得∠AOE=∠COE,根据圆周角定理得到∠B=![]() ∠AOE,∠F=
∠AOE,∠F=![]() ∠COE,得到∠B=∠F,根据等腰三角形的性质得到∠B=∠OEB,于是得到∠F=∠OEG,根据三角形的外角的性质即可得到结论;
∠COE,得到∠B=∠F,根据等腰三角形的性质得到∠B=∠OEB,于是得到∠F=∠OEG,根据三角形的外角的性质即可得到结论;
(3)由圆周角定理得到∠ECF=90°求得OA=OE=![]() EF=
EF=![]() , 设DE=m,AD=2m,根据勾股定理列方程得到m1=0(舍去),m2=
, 设DE=m,AD=2m,根据勾股定理列方程得到m1=0(舍去),m2=![]() , 于是得到DA=DA=
, 于是得到DA=DA=![]()
![]() , DO=
, DO=![]()
![]() , 在Rt△ADO中,tan∠DOA=
, 在Rt△ADO中,tan∠DOA=![]() =
=![]() , cos∠DOA=
, cos∠DOA=![]() =
=![]() , 得到tan∠EGC=
, 得到tan∠EGC=![]() , 过点E作EH⊥AB于点H,在Rt△EOH中OH=OEcos∠EOH=
, 过点E作EH⊥AB于点H,在Rt△EOH中OH=OEcos∠EOH=![]() X
X![]() =
=![]()
![]() , 于是得到EH=
, 于是得到EH=![]()
![]() AH=AO﹣OH=
AH=AO﹣OH=![]() -
-![]()
![]() =
=![]()
![]() , 根据勾股定理求得EC=2,根据三角函数的定义即可得到结论.
, 根据勾股定理求得EC=2,根据三角函数的定义即可得到结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)某种手机卡的市话费上次已按原收费标准降低了m元/分钟,现在再次下调20%,使收费标准为n元/分钟,那么原收费标准为____元/分钟;
(2)买一个篮球需要m元,买一个排球需要n元,则买3个篮球和5个排球共需要____元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小李按市场价格30元/千克收购了一批海鲜1000千克存放在冷库里,据预测,海鲜的市场价格将每天每千克上涨1元.冷冻存放这批海鲜每天需要支出各种费用合计310元,而且这些海鲜在冷库中最多存放160天,同时平均每天有3千克的海鲜变质.
(1)设x天后每千克该海鲜的市场价格为y元,试写出y与x之间的函数关系式;
(2)若存放x天后,将这批海鲜一次性出售.设这批海鲜的销售总额为P元,试写出P与x之间的函数关系式;
(3)小李将这批海鲜存放多少天后出售可获得最大利润,最大利润是多少元?(利润W=销售总额﹣收购成本﹣各种费用) -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x、y的多项式(m﹣2)
 +(n+3)xy2+3xy﹣5.
+(n+3)xy2+3xy﹣5.(1)若原多项式是五次多项式,求m、n的值;
(2)若原多项式是五次四项式,求m、n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点0为坐标原点,抛物线y=ax2+bx+4与y轴交于点A,与x轴交于点B、C(点B在点C左侧),且OA=OC=4OB.
(1)求a,b的值;
(2)连接AB、AC,点P是抛物线上第一象限内一动点,且点P位于对称轴右侧,
过点P作PD⊥AC于点E,分别交x、y轴于点D、H,过点P作PG∥AB交AC于点F,交x轴于点G,设P(x,y),线段DG的长为d,求d与x之间的函数关系(不要求写出自变量x的取值范围);
(3)在(2)的条件下,当 时,连接AP并延长至点M,连接HM交AC于点S,点R是抛物线上一动点,当△ARS为等腰直角三角形时.求点R的坐标和线段AM的长.
时,连接AP并延长至点M,连接HM交AC于点S,点R是抛物线上一动点,当△ARS为等腰直角三角形时.求点R的坐标和线段AM的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2015年6月27日,四川共青图雨城区委在中里镇文化馆举办了第二期青年剪纸培训,参加培训的小王想把一块Rt△ABC废纸片剪去一块矩形BDEF纸片,如图所示,若∠C=30°,AB=10cm,则该矩形BDEF的面积最大为( )

A.4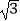 cm3
cm3
B.5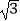 cm3
cm3
C.10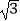 cm3
cm3
D.25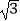 cm3
cm3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3,先让圆周上数字0所对应的点与数轴上的数-2所对应的点重合,再让圆沿着数轴按顺时针方向滚动,那么数轴上的数-2017将与圆周上的哪个数字重合( )
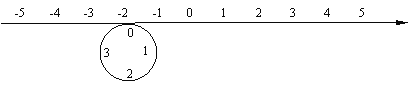
A. 0 B. 1 C. 2 D. 3
相关试题

