【题目】如图,在平面直角坐标系中,点0为坐标原点,抛物线y=ax2+bx+4与y轴交于点A,与x轴交于点B、C(点B在点C左侧),且OA=OC=4OB.
(1)求a,b的值;
(2)连接AB、AC,点P是抛物线上第一象限内一动点,且点P位于对称轴右侧,
过点P作PD⊥AC于点E,分别交x、y轴于点D、H,过点P作PG∥AB交AC于点F,交x轴于点G,设P(x,y),线段DG的长为d,求d与x之间的函数关系(不要求写出自变量x的取值范围);
(3)在(2)的条件下,当![]() 时,连接AP并延长至点M,连接HM交AC于点S,点R是抛物线上一动点,当△ARS为等腰直角三角形时.求点R的坐标和线段AM的长.
时,连接AP并延长至点M,连接HM交AC于点S,点R是抛物线上一动点,当△ARS为等腰直角三角形时.求点R的坐标和线段AM的长.
参考答案:
【答案】解:(1)y=ax2+bx+4,当x=0时,y=4,
∴A(0,4)
∵OC=OA=4OB,
∴OC=4,OB=1,
∴C(4,0),B(﹣1,0)
将C(4,0),B(﹣1,0)代入抛物线y=ax2+bx+4
得:![]() ,解得:
,解得:![]()
∴a=﹣1 b=3.
(2)如图1,作PK⊥x轴于点K.
∵a=﹣1 b=3.
∴抛物线的解析式为y=﹣x2+3x+4.
设点P的坐标为(x,y)
∵OA=OC,∠AOC=90°,
∴∠ACO=45°,
∵AC⊥PD,
∴∠EDC=45°,
∵PK⊥x轴,
∴△PDK为等腰直角三角形,
∴PK=DK=y,
∵AB∥PG,
∴∠ABO=∠PGK,
∵tan∠ABO=![]() =4,
=4,
∴tan∠PGK=![]() =4
=4
∴GK=![]() PK=
PK=![]() y
y
∴d=DK﹣GK=y﹣![]() y=
y=![]() y,
y,
将y=﹣x2+3x+4代入得:d=![]() (﹣x2+3x+4)=-
(﹣x2+3x+4)=-![]() .
.
(3)如图2所示:过点P作PK⊥x轴,垂足为K,PK交于AC与N.
∵![]()
∴![]() .
.
设点P的坐标为(x,y).
∵CK=NK=4﹣x
∴PN=y﹣4+x
∴PE=![]() PN=
PN=![]() (y-4+x),PD=
(y-4+x),PD=![]() PK=
PK=![]() y
y
∴![]() ,
,![]() .
.
将y=﹣x2+3x+4代入得:![]() .
.
整理得:x2﹣7x+12=0.
解得:x1=3,x2=4(舍去).
∴P(3,4)
∵DK=PK=4,
∴D(﹣1,0).
∴点D、B重合.
∵△BOH为等腰直角三角形,
∴OH=OB=1.
∴AH=3.
如图3所示:∠RAS=90°时.
设点R(a,﹣a2+3a+4)
∵△ARS为等腰直角三角形
∴∠RAS=90°,∠ARS=45°
∵AP∥x轴
∴∠PAC=∠ACO=45°.
∴∠RAP=45°.
∴RS⊥AM.
∴AL=LS,AL=LR.
∴a=﹣a2+3a+4﹣4.
∴a=2.
∴R(2,6).
在Rt△LMS中tan∠M=![]() ,在Rt△AHM中tan∠M=
,在Rt△AHM中tan∠M=![]()
∴![]() =
=![]() .
.
∴![]()
∴LM=4
∴AM=6.
当∠ARS=90°和∠ASR=90°时,△ARS不能构成等腰直角三角形.
综上所述,AM的长为6.
【解析】(1)将x=0代入求得y=4,从而得到点A的坐标为(0,4),由OA=OC=4OB可求得C(4,0),B(﹣1,0),然后将点B、C的坐标代入抛物线的解析式可求得a=﹣1,b=3;
(2)作PK⊥x轴于点K.由题意可知△AOC为等腰直角三角形,于是得到∠ACO=45°,由AC⊥PD可证明∠EDC=45°,从而得到△PDK为等腰直角三角形,故此PK=DK=y,由AB∥PG可知∠ABO=∠PGK,由锐角三角函数的定义可知![]() =
=![]() =4,从而得到GK=
=4,从而得到GK=![]() PK=
PK=![]() y,由d=DK﹣GK可求得d=-
y,由d=DK﹣GK可求得d=-![]() ;
;
(3)如图2所示:过点P作PK⊥x轴,垂足为K,PK交于AC与N.由题意可知:![]() , 设点P的坐标为(x,y),由△NKC为等腰直角三角形可知CK=NK=4﹣x,由PN=PK﹣KN可知PN=y﹣4+x,由△PEN为等腰三角三角形可知PE=
, 设点P的坐标为(x,y),由△NKC为等腰直角三角形可知CK=NK=4﹣x,由PN=PK﹣KN可知PN=y﹣4+x,由△PEN为等腰三角三角形可知PE=![]() PN=
PN=![]() (y-4+x),由△PBK为等腰直角三角形可知PD=
(y-4+x),由△PBK为等腰直角三角形可知PD=![]() PK=
PK=![]() y,从而可得到
y,从而可得到![]() ,
, ![]() 将y=﹣x2+3x+4代入得:
将y=﹣x2+3x+4代入得:![]() . 解得:x1=3,x2=4(舍去)于是可求得P(3,4),从而得打D(﹣1,0),故此点D、B重合,由△BOH为等腰直角三角形,可求得AH=3.如图3所示:∠RAS=90°时.设点R(a,﹣a2+3a+4)由△ARS为等腰直角三角形,可证明RS⊥AM,从而得到AL=LS,AL=LR,故此a=﹣a2+3a+4﹣4可求得R(2,6).由锐角三角函数的定义可知:
. 解得:x1=3,x2=4(舍去)于是可求得P(3,4),从而得打D(﹣1,0),故此点D、B重合,由△BOH为等腰直角三角形,可求得AH=3.如图3所示:∠RAS=90°时.设点R(a,﹣a2+3a+4)由△ARS为等腰直角三角形,可证明RS⊥AM,从而得到AL=LS,AL=LR,故此a=﹣a2+3a+4﹣4可求得R(2,6).由锐角三角函数的定义可知:![]() =
=![]() , 从而得到
, 从而得到![]() , 解得LM=4,于是可求得AM=6;当∠ARS=90°和∠ASR=90°时,△ARS不能构成等腰直角三角形,故此AM的长为6.
, 解得LM=4,于是可求得AM=6;当∠ARS=90°和∠ASR=90°时,△ARS不能构成等腰直角三角形,故此AM的长为6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小李按市场价格30元/千克收购了一批海鲜1000千克存放在冷库里,据预测,海鲜的市场价格将每天每千克上涨1元.冷冻存放这批海鲜每天需要支出各种费用合计310元,而且这些海鲜在冷库中最多存放160天,同时平均每天有3千克的海鲜变质.
(1)设x天后每千克该海鲜的市场价格为y元,试写出y与x之间的函数关系式;
(2)若存放x天后,将这批海鲜一次性出售.设这批海鲜的销售总额为P元,试写出P与x之间的函数关系式;
(3)小李将这批海鲜存放多少天后出售可获得最大利润,最大利润是多少元?(利润W=销售总额﹣收购成本﹣各种费用) -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x、y的多项式(m﹣2)
 +(n+3)xy2+3xy﹣5.
+(n+3)xy2+3xy﹣5.(1)若原多项式是五次多项式,求m、n的值;
(2)若原多项式是五次四项式,求m、n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:AB是⊙O的直径,DA、DC分别是⊙O的切线,点A、C是切点,连接DO交弧AC于点E,连接AE、CE.

(1)如图1,求证:EA=EC;
(2)如图2,延长DO交⊙O于点F,连接CF、BE交于点G,求证:∠CGE=2∠F;
(3)如图3,在(2)的条件下,DE= AD,EF=2
AD,EF=2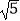 , 求线段CG的长.
, 求线段CG的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】2015年6月27日,四川共青图雨城区委在中里镇文化馆举办了第二期青年剪纸培训,参加培训的小王想把一块Rt△ABC废纸片剪去一块矩形BDEF纸片,如图所示,若∠C=30°,AB=10cm,则该矩形BDEF的面积最大为( )

A.4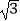 cm3
cm3
B.5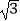 cm3
cm3
C.10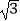 cm3
cm3
D.25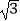 cm3
cm3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3,先让圆周上数字0所对应的点与数轴上的数-2所对应的点重合,再让圆沿着数轴按顺时针方向滚动,那么数轴上的数-2017将与圆周上的哪个数字重合( )
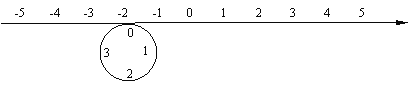
A. 0 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,D,E为BC上两点,过点D,E分别作AC,AB的垂线,两垂线交于点M,垂足分别为G,F,若∠AED=∠BAD,AB=AC=2,则下列说法中不正确的是( )

A.△CAE∽△BDA
B.
C.BD?CE=4
D.BE= BF
BF
相关试题

